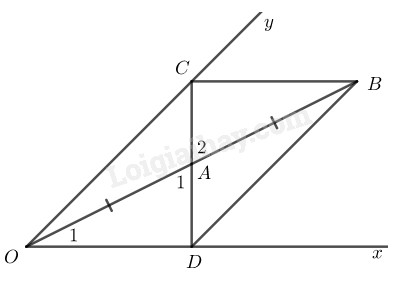
\(a)\) Xét \(∆ OAD\) và \(∆ BAC:\)
\(OA = AB\) (tính chất đối xứng tâm)
\({\widehat A_1} = {\widehat A_2}\) (đối đỉnh)
\({\widehat O_1} = {\widehat B_1}\) (so le trong)
Do đó: \(∆ OAD = ∆ BAC \;\;(g.c.g)\)
\(⇒ AD = AC\)
Suy ra: \(C\) đối xứng với \(D\) qua tâm \(A.\)
\(b)\) Cách dựng :
- Dựng \(B\) đối xứng với \(O\) qua tâm \(A\)
- Qua \(B\) dựng đường thẳng song song \(Ox\) cắt \(Oy\) tại \(C.\)
- Dựng tia \(CA\) cắt \(Ox\) tại \(D.\)
Ta có \(D\) là điểm cần dựng.
Chứng minh : như câu \(a)\)