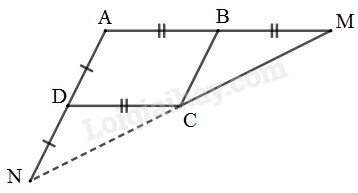
Tứ giác \(ABCD\) là hình bình hành
\(⇒ AB // CD\) hay \(BM // CD\)
Xét tứ giác \(BMCD\) ta có:
\(BM // CD\)
\(BM = CD\;\; (gt)\)
Suy ra: Tứ giác \(BMCD\) là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
\(⇒ MC // BD\) và \(MC = BD \;\;(1)\)
\(AD // BC \;\;( gt)\) hay \(DN // BC\)
Xét tứ giác \(BCND\) ta có:
\(DN // BC\)
\(DN = BC\) (vì cùng bằng \(AD\))
Suy ra: Tứ giác \(BCND\) là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
\(⇒ CN // BD\) và \(CN = BD\;\; (2)\)
Từ \((1)\) và \((2)\) suy ra: \(M, C, N\) thẳng hàng và \(MC = CN\)
Vậy \(M\) và \(N\) đối xứng qua tâm \(C.\)