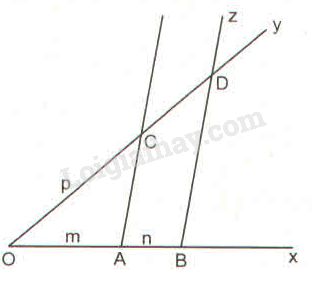
Cách dựng:
- Dựng hai tia chung gốc \(Ox\) và \(Oy \) phân biệt không đối nhau.
- Trên tia \(Ox\) dựng đoạn \(OA = m\) và dựng đoạn \(AB = n\) sao cho \(A\) nằm giữa \(O\) và \(B.\)
- Trên tia \(Oy\) dựng đoạn \(OC = p.\)
- Dựng đường thẳng \(AC\)
- Từ \(B\) dựng đường thẳng song song với \(AC\) cắt tia \(Oy\) tại \(D.\) Ta được đoạn thẳng \(CD = q\) cần dựng.
Chứng minh:
Theo cách dựng, ta có \(AC // BD.\)
Xét \(∆ OBD\) có \(AC // BD\)
Theo định lí Ta-lét ta có:
\(\displaystyle {{OA} \over {AB}} = {{OC} \over {CD}}\)
Vậy \(\displaystyle {m \over n} = {p \over q}\).