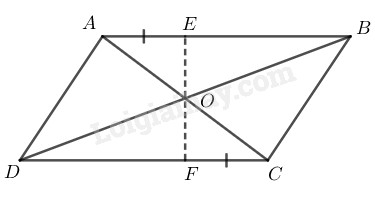
Gọi \(O\) là giao điểm của hai đường chéo \(AC\) và \(BD.\)
Xét tứ giác \(AECF:\)
\(AB // CD\;\; (gt)\)
\(⇒ AE // CF\)
\(AE = CF\;\; (gt)\)
Suy ra: Tứ giác \(AECF\) là hình bình hành ( vì có một cặp cạnh đối song song và bằng nhau)
\(⇒ AC\) và \(EF\) cắt nhau tại trung điểm mỗi đường
\(OA = OC\) ( tính chất hình bình hành)
\(⇒ EF\) đi qua \(O\)
Vậy \(AC, BD, EF\) đồng quy tại \(O.\)