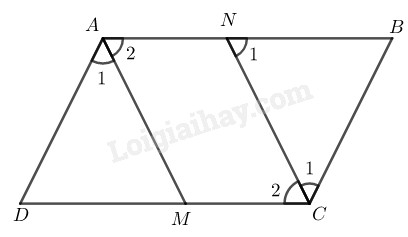
Ta có: \(\widehat A = \widehat C\) (tính chất hình bình hành)
\(\eqalign{ & {\widehat A_2} = {1 \over 2}\widehat A(gt) \cr & {\widehat C_2} = {1 \over 2}\widehat C(gt) \cr} \)
Suy ra: \(\widehat A_2=\widehat C_2\)
\(AB // CD\;\; (gt)\)
hay \(AN // CM \;\;(1)\)
Mà \({\widehat N_1} = {\widehat C_2}\) (so le trong)
Suy ra: \({\widehat A_2} = {\widehat N_1}\)
\(⇒ AM // CN \) ( vì có các cặp góc ở vị trí đồng vị bằng nhau) \((2)\)
Từ \((1)\) và \((2)\) suy ra: Tứ giác \(AMCN\) là hình bình hành ( theo định nghĩa)