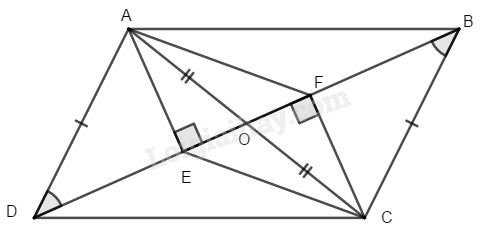
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\(OA = OC\) ( tính chất hình bình hành) \((1)\)
Xét hai tam giác vuông \(AEO\) và \(CFO,\) ta có:
\(\widehat {AEO} = \widehat {CFO} = {90^0}\)
\(OA = OC\) ( chứng minh trên)
\(\widehat {AOE} = \widehat {COF}\) (đối đỉnh)
Do đó \(∆ AEO =∆ CFO\) ( cạnh huyền, góc nhọn)
\(⇒ OE = OF \;\;(2)\)
Từ \((1)\) và \((2)\) suy ra tứ giác \(AECF\) là hình bình hành ( vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)