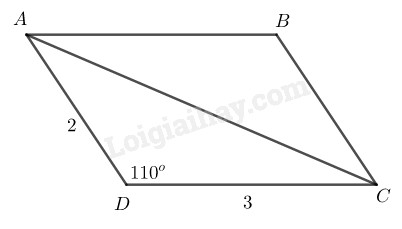
\(a)\) Cách dựng:
Dựng \(∆ ABD\) có \(AB = 2cm,\) \(\widehat A = {110^0},\) \(AD = 3cm\)
- Dựng tia \(Bx // AD\)
- Dựng tia \(Dy // AB\) cắt \(Bx\) tại \(C\)
Ta có hình bình hành \(ABCD\) cần dựng
Chứng minh: \(AB // CD,\) \(AD // BC\) nên tứ giác \(ABCD\) là hình bình hành.
Ta lại có \(AB = 2cm,\) \(\widehat A = {110^0},\) \(AD = 3cm.\) Bài toán có một nghiệm hình.
\(b)\)
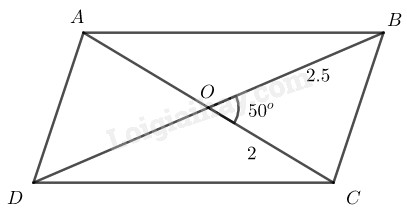
Cách dựng:
- Dựng \(∆ OBC\) có \(OC = 2cm,\) \(OB = 2,5cm ,\) \(\widehat O = {50^0}\)
- Trên tia đối tia \(OC\) lấy điểm \(A\) sao cho \(OA = OC = 2cm\)
- Trên tia đối tia \(OB\) lấy điểm \(D\) sao cho \(AD = OB = 2,5cm\)
Nối \(AB, BC, CD, AD\) ta có hình bình hành \(ABCD\) cần dựng
Chứng minh: Tứ giác \(ABCD\) có \(OA = OC,\) \(OB = OD\) nên nó là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Có \(AC = 4cm,\) \(BD = 5cm,\) \(\widehat {BOC} = {50^0}\)
Bài toán có một nghiệm hình.