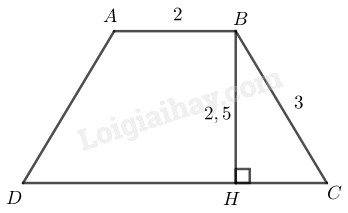
Cách dựng:
- Dựng \(∆ BHC,\) \(BH = 2,5 cm\)
- \(\widehat {BHC} = {90^0}\)
- \(BC = 3cm\)
- Dựng tia đi qua \(B\) và song song \(CH\) nằm trên nửa mặt phẳng bờ \(BC\) chứa điểm \(H.\) Lấy điểm \(A\) sao cho \(BA = 2cm\)
- Dựng cung tròn tâm \(B\) bán kính bằng \(AC\) cắt đường thẳng \(CH\) tại \(D.\)
Nối \(AD\) ta có hình thang \(ABCD\) cần dựng.
Chứng minh:
Thật vậy theo cách dựng \(AB // CD\) nên tứ giác \(ABCD\) là hình thang có \(AB = 2cm,\) \(BC = 3cm,\) \(BH = 2,5cm,\)\(AC = BD\)
Vậy \(ABCD\) là hình thang cân thỏa mãn điều kiện bài toán.
Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.