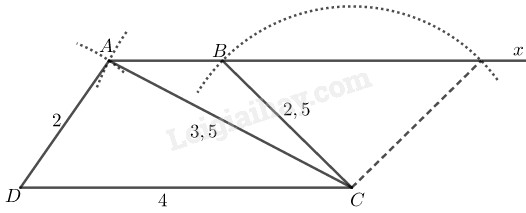
Phân tích: Giả sử hình thang \(ABCD\) dựng được thỏa mãn điều kiện bài toán. Tam giác \(ADC\) dựng được vì biết ba cạnh \(AD = 2cm,\) \(DC = 4cm,\) \(AC = 3,5cm.\)
Điểm \(B\) thỏa mãn hai điều kiện:
- \(B\) nằm trên đường thẳng đi qua \(A\) và song song với \(CD.\)
- \(B\) cách \(C\) một khoảng bằng \(2,5cm\)
Cách dựng:
- Dựng \(∆ ADC\) biết \(AD = 2cm,\) \(DC = 4cm,\) \(AC = 3,5cm\)
- Dựng tia \(Ax // CD.\) \(Ax\) nằm trong nửa mặt phẳng bờ \(AD\) chứa điểm \(C.\)
- Dựng cung tròn tâm \(C\) bán kính \(2,5cm.\) Cung này cắt \(Ax\) tại \(B,\) nối \(CB\) ta có hình thang \(ABCD\) cần dựng.
Chứng minh:
Tứ giác \(ABCD\) là hình thang vì \(AB // CD\)
Hình thang \(ABCD\) có: \(AD = 2cm,\) \(CD = 4cm,\) \(AC = 3,5cm,\) \(BC = 2,5cm\) thỏa mãn yêu cầu bài toán.
Biện luận: \(∆ ADC\) luôn dựng được nên hình thang \(ABCD\) dựng được.
Vì cung tròn tâm \(C\) bán kính \(3cm\) cắt \(Ax\) tại hai điểm ta dựng được hai hình thang thỏa mãn bài toán.