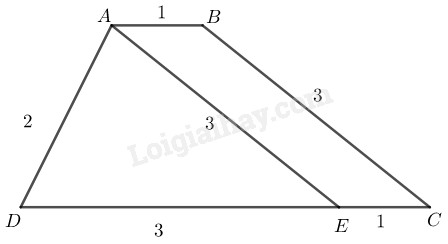
Phân tích: Giả sử hình thang \(ABCD\) dựng được thỏa mãn điều kiện bài toán.
Qua \(A\) kẻ đường thẳng song song với \(BC\) cắt \(CD\) tại \(E\) ta thấy tam giác \(AED\) xác định vì biết ba cạnh, ta cần xác định đỉnh \(B\) và \(C\)
- Đỉnh \(C\) nằm trên tia \(DE,\) cách \(D\) một khoảng bẳng \(4cm\)
- Đỉnh \(B\) nằm trên đường thẳng đi qua \(A\) song song với đường thẳng \(DE\) và cách \(A\) một khoảng bằng \(1cm.\)
Cách dựng:
- Dựng \(∆ ADE\) biết \(AD = 2cm,\) \(DE = 3cm,\) \(AE = 3cm\)
- Trên tia \(DE\) dựng điểm \(C\) sao cho \(DC = 4cm\)
- Dựng đường thẳng đi qua \(A\) và song song với \(DC,\) lấy điểm \(B\) sao cho \(AB = 1cm.\) Nối \(BC\) ta có hình thang \(ABCD\) cần dựng
Chứng minh: Thật vậy theo cách dựng ta có \(AB // CD\) nên tứ giác \(ABCD\) là hình thang.
Ta có: \(AD = 2cm,\) \(DC = 4cm,\) \(AB = 1cm,\) hình thang \(ABCE\) có hai cạnh đáy \(AB = EC = 1cm\) nên \(BC = AE = 3cm.\)
Hình thang \(ABCD\) thỏa mãn điều kiện bài toán.
Biện luận: Tam giác \(ADE\) luôn dựng được nên hình thang \(ABCD\) dựng được, bài toán có một nghiệm hình.