Bài 1: a) Bảng giá trị \(( y = x^2)\)
|
x
|
− 2
|
− 1
|
0
|
1
|
2
|
|
y
|
4
|
1
|
0
|
1
|
4
|
Đồ thị của hàm số là một parabol (P).
Đồ thị của hàm số là đường thẳng (d) qua hai điểm \(( 0; − 1), (1; 1).\)
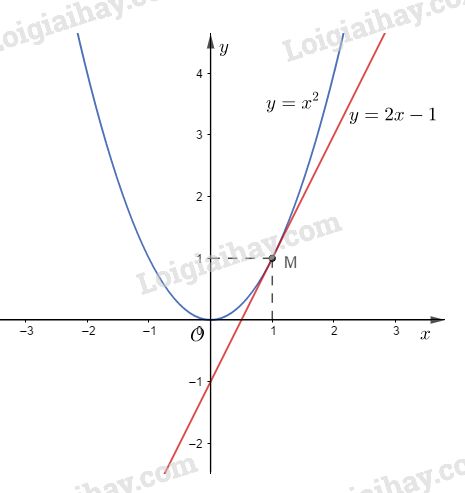
b) Phương trình hoành độ giao điểm của (P) và (d) :
\({x^2} = 2x - 1 \Leftrightarrow {x^2} - 2x + 1 = 0 \)
\(\Leftrightarrow {\left( {x - 1} \right)^2} = 0 \Leftrightarrow x = 1\)
Vậy tọa độ giao điểm của (P) và (d) là \(M(1; 1).\)
Bài 2: Ta có : \({m^2} - 2m + 3 = {m^2} - 2m + 1 + 2\)\(\;={\left( {m - 1} \right)^2} + 2 > 0\), với mọi m ( vì \(( m – 1)^2≥ 0)\)
Vậy hệ số \(a > 0\), với mọi m nên hàm số đã cho đồng biến khi \(x > 0.\)
Ta có : \(0 < \sqrt 2 < \sqrt 5 \Rightarrow f\left( {\sqrt 2 } \right) < f\left( {\sqrt 5 } \right).\)