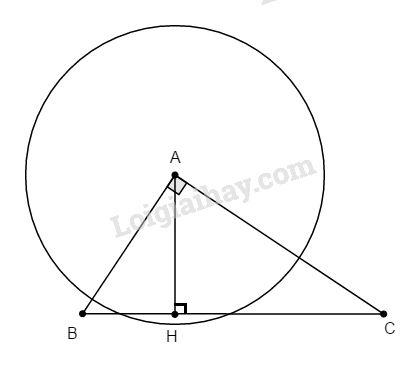
Kẻ \(AH ⊥ BC\). Trong tam giác vuông ABC, ta có: \({1 \over {A{H^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}}\) (định lí 4)
hay \({1 \over {A{H^2}}} = {1 \over {{3^2}}} + {1 \over {{4^2}}} = {{25} \over {144}}\)
\(\Rightarrow {1 \over {AH}} = {5 \over {12}} \Rightarrow AH = 2,4cm\)
Ta có: \(2,4 < 2,8 \;(d < R)\)
Do đó đường thẳng BC và (A; 2,8cm) cắt nhau.