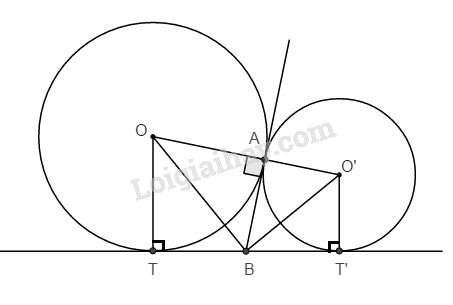
a. Ta có: \(BT = BA\) (tính chất tiếp tuyến cắt nhau).
Tương tự \(BT’ = BA ⇒ BT = BT’\)
b. BO, BO’ là hai tia phân giác của hai góc kề bù \(\widehat {TBA},\widehat {T'BA}\) nên \(\widehat {OBO'} = 90^\circ \)
Mặt khác \(BA ⊥ OO’\) (tính chất tiếp tuyến)
\(∆OBO’\) có BA là đường cao nên \(B{A^2} = OA.O'A = RR'\) (hệ thức lượng)
\( \Rightarrow BA = \sqrt {RR'} \)
Do đó: \(TT' = 2BA = 2\sqrt {RR'} \)