Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 9

Cho nửa đường tròn tâm O đường kính AB. Trên cùng nửa mặt phẳng có bờ là đường thẳng AB, vẽ các tiếp tuyến Ax, By với (O) (A, B là các tiếp điểm). Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt Ax, By lần lượt tại C và D. Gọi N là giao điểm của AD và BC. Chứng minh:

a. \(CD = CA + DB\)

b. \(MN ⊥ AB.\)

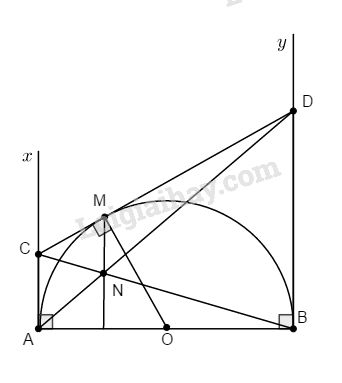
a. Ta có: \(CA = CM, DB = DM\) (tính chất hai tiếp tuyến cắt nhau).

Mà \(CD = CM + MD \)\(\;⇒ CD = CA + DB.\)

b. Ta có: Ax, By là hai tiếp tuyến của (O) nên Ax // By (cùng vuông góc AB)

Theo định lí Ta-lét, ta có:

\(\eqalign{  & {{CA} \over {DB}} = {{NC} \over {NB}}\cr&\text{Mà }\,CA = CM,DB = DM  \cr  &  \Rightarrow {{CM} \over {DM}} = {{NC} \over {NB}} \cr} \)

Theo Định lí Ta-lét đảo \(⇒ MN // BD\)

Mà \(BD ⊥ AB ⇒ MN ⊥ AB.\)