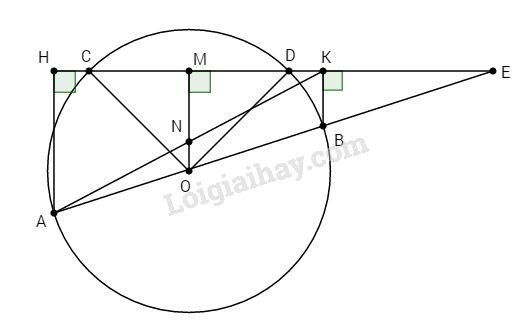
Kẻ \(OM ⊥ CD\), ta có: \(MC = MD\) (1) (định lí đường kính dây cung)
và OM // BK (cùng \(⊥ CD\))
Gọi N là giao điểm của OM và AK, ta có ON là đường trung bình của ∆ABK nên N là trung điểm của AK. Mặt khác trong tam giác vuông AHK ta có MN // AH nên MN là đường trung bình của ∆AHK.
Do đó M là trung điểm của HK
hay \(MH = MK\) (2)
Từ (1) và (2) \(⇒ MC – MH = MD – MK\) hay \(CH = DK\).