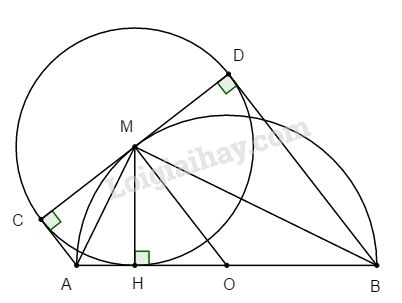
a. Ta có: AC, AH là tiếp tuyến của đường tròn (M; MH) nên MA là phân giác của góc \(\widehat {CMH}\) hay \(\widehat {CMA} = \widehat {AMH}\)
Tương tự MB là phân giác của \(\widehat {DMH} \Rightarrow \widehat {HMB} = \widehat {BMD}\)
mà \(\widehat {AMH} + \widehat {HMB} = \widehat {AMB} = 90^\circ \) (AB là đường kính)
\( \Rightarrow \widehat {CMA} + \widehat {AMH} + \widehat {HMB} + \widehat {BMD}\)\(\, = 180^\circ \) hay ba điểm C, M, D thẳng hàng \(⇒ CA // BD (⊥ CD)\) hay tứ giác ABCD là hình thang vuông, có OM là đường trung bình nên OM // AC // BD \(⇒ OM ⊥ CD.\)
Chứng tỏ CD là tiếp tuyến của (O)
b. Ta có: \(AC = AH, BD = BH\) (tính chất hai tiếp tuyến cắt nhau)
\(⇒ AC + BD = AH + BH = AB\)\( = 2R\) không đổi.