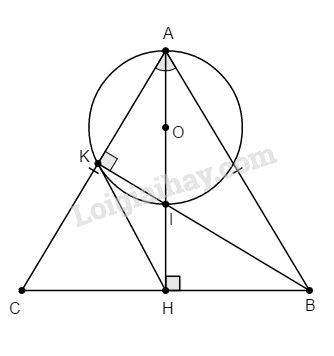
Gọi O là tâm đường tròn đường kính AI. Hiển nhiên K thuộc (O) (vì \(\widehat {AKI} = 90^\circ \) )
∆ABC cân tại A có AH là đường cao (gt) nên AH đồng thời là đường trung tuyến \(⇒ HB = HC.\)
Xét ∆BKC vuông tại K có KH là đường trung tuyến nên \(KH = BH = {{BC} \over 2}\)
Do đó ∆BHK cân tại H \( \Rightarrow {\widehat B_1} = \widehat {BKH}\) (1)
Lại có ∆IOK cân tại O \(\left( {OI = OK = {{AI} \over 2}} \right)\)
\( \Rightarrow {\widehat I_2} = \widehat {OKI},\) mà \({\widehat I_2} = {\widehat I_1}\) (đối đỉnh)
\( \Rightarrow \widehat {OKI} = {\widehat I_1}\) (2)
Mặt khác ∆BHI vuông tại H (gt) nên \({\widehat B_1} + {\widehat I_1} = 90^\circ \) (3)
Từ (1), (2) và (3), ta có: \(\widehat {BKH} + \widehat {OKI} = 90^\circ \) hay \(HK ⊥ OK\).
Vậy HK là tiếp tuyến của đường tròn (O).