Đọc hiểu - Đề số 71 - THPT

I) Trắc nghiệm

Câu 1: Phương trình \(3x + 1 = 0\) có nghiệm là:

A. \(x =  - \dfrac{1}{3}\)       

B. \(x = \dfrac{1}{3}\)

C. \(x =  - 1\)

D. \(x = 1\)

Câu 2: Bất phương trình \(2x - 1 < 5\) có tập nghiệm là:

A. \(S = \left\{ {x|x > 2} \right\}\)

B. \(S = \left\{ {x|x < 2} \right\}\)

C. \(S = \left\{ {x|x < 3} \right\}\)

D. \(S = \left\{ {x|x > 3} \right\}\)

Câu 3: Phương trình \(16{x^2} = 25\) có tập nghiệm là:

A.\(S = \left\{ {\dfrac{{25}}{{16}}} \right\}\)

B. \(S = \left\{ {\dfrac{{16}}{{25}}} \right\}\)       

C. \(S = \left\{ { - \dfrac{4}{5};\dfrac{4}{5}} \right\}\)

D. \(S = \left\{ { - \dfrac{5}{4};\dfrac{5}{4}} \right\}\)

Câu 4: Lăng trụ đứng có đáy là hình thoi, hai đường chéo của đáy bằng 6cm và 8cm, chiều cao của lăng trụ bằng 7cm. Thể tích của lăng trụ là:

A. \(336c{m^3}\)

B. \(168c{m^3}\)

C. \(196c{m^3}\)

D. \(98c{m^3}\)

II) Tự lận

Câu 5 : Giải các phương trình, bất phương trình sau

\(1)\,\,\dfrac{{3x + 5}}{2} < 1\)

\(2)\,\,\dfrac{1}{{x + 2}} + \dfrac{1}{{x - 2}} = \dfrac{6}{{{x^2} - 4}}\)                     

\(3)\,\left| {x - 2} \right| + \left| {2 - x} \right| = 10\)

Câu 6: Giải bài toán bằng cách lập phương trình

Một tàu hỏa cần vận chuyển một lượng hàng. Người lái tàu tính rằng nếu xếp lên mỗi toa 14 tấn hàng thì còn thừa lại 4 tấn, còn nếu muốn xếp lên mỗi toa 16 tấn hàng thì còn thiếu 6 tấn nữa. Hỏi tàu hỏa đó có mấy toa chở hàng?

Câu 7 : Cho tam giác BCD vuông tại B, \(BC < BD.\) Vẽ đường cao BH.

1) Chứng minh rằng tam giác BCD đồng dạng với tam giác HCB. Từ đó suy ra \(CH.CD = C{B^2}\)

2) Cho \(BC = 15,BD = 20\)

   a) Tính độ dài các đoạn thẳng CD, CH

   b) Gọi A là điểm sao cho tứ giác ABCD là hình thang cân có hai cạnh đáy là AB và CD. Tính diện tích hình thang ABCD.

Câu 8 : Giải bất phương trình \(3{x^3} - 5{x^2} - x - 2 > 0\)

I. PHẦN TRẮC NGHIỆM: 

Câu 1 : Cho a> b và a.b<0, bất đẳng thức \(\dfrac{1}{a} > \dfrac{1}{b}\) là đúng hay sai ?

A. Đúng                         B.Sai

Câu 2 : Hai phương trình cùng nhận x= a làm nghiệm có tương đương với nhau không?

A. Có                              B. không

Câu 3: Giải phương trình \(2{x^2} - 2x + 1 =  - 5x\)

A. x= -1

B. x= \(\dfrac{1}{2}\)

C. x= 1

D.x = -1; x= -\(\dfrac{1}{2}\)

Câu 4 : Viết tập  nghiệm  của bất phương trình bằng kí hiệu tập hợp:

                    \( - 7 \ge 5x\)

A. \(S = \left\{ {x \in R/x \le  - \dfrac{7}{5}} \right\}\)

B. \(S = \left\{ {x \in R/x \ge \dfrac{7}{5}} \right\}\)

C. \(S = \left\{ {x \in R/x \le \dfrac{7}{5}} \right\}\)

D.\(S = \left\{ {x \in R/x \ge  - \dfrac{7}{5}} \right\}\)

Câu 5 : Cho hình hộp chữ nhật có ba kích thước 5cm,3cm,2cm. Tính thể tích của hình hộp đó>

A. 30cm

B. 30 cm²

C. 10cm ³

D. 30cm³

Câu 6 :  Tính tỉ số của các cặp đoạn thẳng sau :

AB=18cm,CD =12cm

A.\(\dfrac{5}{3}\)

B. \(\dfrac{3}{2}\)

C.\(\dfrac{1}{6}\)

D.\(\dfrac{{12}}{{15}}\)

 II. PHẦN TỰ LUẬN :

Bài 1:  Cho biểu thức :  M = \(\left( {\dfrac{1}{{x + 1}} + \dfrac{2}{{1 - x}} + \dfrac{x}{{{x^2} - 1}}} \right):\dfrac{1}{{x + 1}}\)

  a, Rút gọn biểu thức M.

  b, Tính giá trị của biểu thức M khi x = -1 ; x = 2

Bài 2: 

  a, Giải bất phương trình và biểu diễn tập nghiệm trên trục số :  3x – 12 ≥ 0 

  b, Cho ba số dương a, b, c có tổng bằng 1. Chứng minh : \(\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge 9\)

Bài 3: 

   Một xe ô tô đi từ A đến B với vận tốc 50 km/h . Lúc từ B trở về A xe đi với vận tốc 45km/h nên thời gian về nhiều hơn thời gian đi là 20 phút. Tính quãng đường AB.

Bài 4:

  Cho hình chữ nhật ABCD , có AB = 3 cm , BC = 4 cm . Vẽ đường cao AH của tam giác ABD .

   a, Chứng minh: ∆AHD ~ ∆DCB.

   b, Chứng minh: AB² = BH.BD .

   c, Tính độ dài: BH, AH .

I. Trắc nghiệm: 

Đọc kĩ các câu hỏi và chọn đáp án đúng của các câu trả lời đã cho ở bên dưới. Ví dụ: Câu 1 chọn đáp án A thì ghi là: 1A…

Câu 1. Cho \(\left| a \right|\, = \,5\)thì:

A. a = 5.

B. a = - 5.

C. a = \( \pm \)5.

D. Một đáp án khác.

Câu 2. Hình hộp chữ nhật là hình có bao nhiêu mặt ?

A. 6 mặt.

B. 5 mặt.

C. 4 mặt.

D. 7 mặt.

Câu 3. Điều kiện xác định của phương trình \(\dfrac{x}{{x + 3}} - \dfrac{{x - 1}}{x} = 1\) là:

A. x\( \ne \)0.

B. x\( \ne \)3.

C.  x\( \ne \)0 và x\( \ne \)3.

D. x\( \ne \)0 và x\( \ne \)-3.         

Câu 4. Bất phương trình nào sau đây là bất phương trình bậc nhất một ẩn ?

A. x + y > 2.

B.  0.x – 1 \( \ge \) 0.

C.   2x –5 >  1.           

D. (x – 1)² \( \le \) 2x.

Câu 5. Nghiệm của bất phương trình 6 – 3x < 15 là:

A.  x >– 5.

B. x <– 5.

C.  x < –3.

D.  x > –3.

Câu 6. Hình sau biểu diễn tập nghiệm của bất phương trình nào?

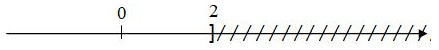
A. x ≤ 2.

B. x > 2.

C. x ≥ 2.

D. x <2. 

Câu 7. Trong các phương trình sau, phương trình nào không có một nghiệm duy nhất ? 

A. 8 + x = 4.

B. 2 – x = x – 4.

C. 1 + x =  x.

D. 5 + 2x = 0.

Câu 8. Nếu tam giác ABC có MN//BC, \((M \in AB,N \in AC)\) theo định lý Talet ta có:

A.  \(\dfrac{{AM}}{{MB}} = \dfrac{{AN}}{{NC}}\).

B. \(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{NC}}\).

C. \(\dfrac{{AM}}{{MB}} = \dfrac{{AN}}{{AC}}\).

D.\(\dfrac{{AB}}{{MB}} = \dfrac{{AN}}{{NC}}\).

Câu 9.  Phương trình nào sau đây là phương trình bậc nhất một ẩn ?

A. 0x + 2 = 0.

B.\(\dfrac{x}{{{x^2} + 1}}.\)

C. x + y = 0.

D. 2x + 1 = 0.

Câu 10.  Nếu \(\Delta\) MNP đồng dạng \(\Delta\) DEF thì ta có tỉ lệ thức nào đúng nhất ?

A. \(\dfrac{{MN}}{{DE}} = \dfrac{{MP}}{{DF}}\).

B. \(\dfrac{{MN}}{{DE}} = \dfrac{{NP}}{{EF}}\).

C.  \(\dfrac{{NP}}{{DE}} = \dfrac{{{\rm{EF}}}}{{MN}}\).

D. \(\dfrac{{MN}}{{DF}} = \dfrac{{NP}}{{{\rm{EF}}}} = \dfrac{{MP}}{{DE}}\).

Câu 11. Dựa vào hình vẽ trên cho biết, x =  ?                              

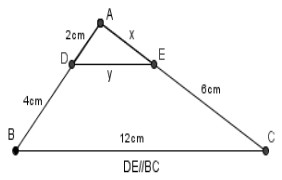
A. 9cm.

B. 6cm.

C. 1cm.

D. 3cm.

Câu 12. Tập nghiệm của phương trình x – 1 = 0 là:

A. {0} .

B. {1}.

C. {1;0}.

D. {–1}.                       

II. Tự luận:

Câu 1. 

a) Giải phương trình: (3x – 2)(4x + 5) = 0.

b) Giải bất phương trình sau và biểu diễn tập hợp nghiệm trên trục số: \(\dfrac{{2x - 3}}{2} > \dfrac{{8x - 11}}{6}.\)

Câu 2. 

Học kì I, số học sinh giỏi của lớp 8 A bằng \(\dfrac{1}{8}\) số học sinh cả lớp. Sang học kì II, có thêm 3 bạn phấn đấu trở thành học sinh giỏi nữa, do đó số học sinh giỏi bằng 20% số học sinh cả lớp. Hỏi lớp 8A có bao nhiêu học sinh ?

Câu 3.

Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm, AD là tia phân giác góc A \(({\rm{D}} \in {\rm{BC}}\)).

a. Tính \(\dfrac{{{\rm{DB}}}}{{{\rm{DC}}}}\) .

b. Kẻ đường cao AH (\({\rm{H}} \in {\rm{BC}}\)). Chứng minh rằng: \({\rm{\Delta AHB}}\) đồng dạng \({\rm{\Delta CHA}}\).

c.Tính: \(\dfrac{{{S_{\Delta AHB}}}}{{{S_{\Delta CHA}}}}.\)

Phần I- Trắc nghiệm :

Từ câu 1 đến câu 8: hãy chọn đáp án đúng và viết vào bài làm.

Câu 1: Phương trình bậc nhất một ẩn  \(ax + b = 0\) ( a ≠ 0) có nghiệm duy nhất là

A. \(x = \dfrac{a}{b}\)

B. \(x = \dfrac{{ - b}}{a}\)

C. \(x = \dfrac{{ - a}}{b}\)

D. \(x = \dfrac{{ - b}}{{ - a}}\)

Câu 2: Điều kiện xác định của phương trình \(\dfrac{{x + 2}}{x} - \dfrac{x}{{x + 1}} = \dfrac{5}{{x\left( {x + 1} \right)}}\) là

A.  \(x \ne 0\)

B.  \(x \ne 0\) và \(x \ne  - 2\)

C.  \(x \ne 0\) và \(x \ne  - 1\)

D.  \(x \ne  - 1\) và \(x \ne  - 2\)

Câu 3: Giá trị  x = -3 là một  nghiệm của bất phương trình nào sau đây ? 

A. \(1 - 2{\rm{x < 2x - 1}}\)

B.  \(x + 7 > 10 + 2{\rm{x}}\)

C. \({\rm{x - 3 > 0}}\)

D.  \(x + 3 \ge 0\)

Câu 4: Trong \(\Delta ABC\) có MN//BC \(\left( {M \in AB;\,N \in AC} \right)\), ta có tỉ số

A.\(\dfrac{{MA}}{{MC}} = \dfrac{{{\rm{NB}}}}{{{\rm{NA}}}}\)

B. \(\dfrac{{MA}}{{NC}} = \dfrac{{{\rm{MB}}}}{{{\rm{NA}}}}\)

C.\(\dfrac{{MA}}{{MB}} = \dfrac{{{\rm{NA}}}}{{{\rm{NC}}}}\)

D.\(\dfrac{{MA}}{{MB}} = \dfrac{{{\rm{NB}}}}{{{\rm{NC}}}}\)

Câu 5: Tập nghiệm của phương trình \(\left( {{x^2} - 4} \right)\left( {{x^2} + 1} \right) = 0\) là

A. \({\rm{S = }}\left\{ {{\rm{ - 2;}}\,{\rm{2}}} \right\}\)

B. \({\rm{S = }}\left\{ {{\rm{ - 1;}}\,{\rm{2}}} \right\}\)

C. \({\rm{S = }}\left\{ {{\rm{ - 1; - }}\,{\rm{2;}}\,{\rm{2}}} \right\}\)

D. \({\rm{S = }}\left\{ {{\rm{ - 1;}}\,{\rm{1;}}\,{\rm{ - 2;}}\,{\rm{2}}} \right\}\)

Câu 6: Cho \(\Delta ABC\) có đường phân giác trong AD, ta có tỉ số

A.  \(\dfrac{{AB}}{{B{\rm{D}}}} = \dfrac{{{\rm{DC}}}}{{{\rm{AC}}}}\)

B.   \(\dfrac{{DB}}{{DC}} = \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\)

C.   \(\dfrac{{DC}}{{B{\rm{D}}}} = \dfrac{{{\rm{AB}}}}{{{\rm{AC}}}}\)

D.   \(\dfrac{{AB}}{{AC}} = \dfrac{{{\rm{DC}}}}{{{\rm{DB}}}}\)

Câu 7: \(\Delta ABC\) đồng dạng với \(\Delta D{\rm{EF}}\) theo tỉ số đồng dạng \(k = \dfrac{3}{2}\). Diện tích của \(\Delta ABC\) là \(27c{m^2}\), thì diện tích của \(\Delta D{\rm{EF}}\) là

A. \(12c{m^2}\)

B. \(24c{m^2}\)

C. \(36c{m^2}\)

D. \(48c{m^2}\)

Câu 8: Một hình lập phương có diện tích toàn phần là \(216c{m^2}\), thể tích của khối lập phương đó là

A. \({\rm{ 72c}}{{\rm{m}}^{\rm{3}}}\)

B.   \({\rm{ 36c}}{{\rm{m}}^{\rm{3}}}\)

C.  \({\rm{ 1296c}}{{\rm{m}}^{\rm{3}}}\)

D.   \({\rm{ 216c}}{{\rm{m}}^{\rm{3}}}\)

Phần II- Tự luận :

Câu 9 :   Giải các phương trình sau:

\(a)\,\,\,\,\,\,\,4x - 3\left( {x - 2} \right) = 7 - x\)

\(b)\,\,\,\,\,\,\,\dfrac{x}{{x - 2}} - \dfrac{{x - 1}}{{x + 2}} = \dfrac{3}{{{x^2} - 4}}\).

Câu 10: Một ôtô xuất phát từ A lúc 5h và dự định đi đến B lúc 12h cùng ngày. Ôtô đi hai phần ba đoạn đường đầu với vận tốc trung bình 40 km/h. Để đến B đúng dự định ôtô phải tăng vận tốc thêm 10 km/h trên đoạn đường còn lại. Tính độ dài quãng đường AB?

Câu 11:  Cho hình thang ABCD vuông tại A và D có đường chéo DB vuông góc với cạnh bên BC tại B, biết AD = 3 cm, AB = 4 cm.

a) Chứng minh Δ ABD đồng dạng với Δ BDC.

b) Tính độ dài DC.

c) Gọi E là giao điểm của AC với BD. Tính diện tích \(\Delta A{\rm{ED}}\).

Câu 12 :

a) Giải phương trình \(\left| { - 7{\rm{x + 1}}} \right| - 16 =  - 8{\rm{x}}\)

b) Cho các số dương x, y thỏa mãn \(x + y =1.\) Tìm giá trị nhỏ nhất của  \({\rm{P  =  }}{\left( {{\rm{2x}} + \dfrac{{\rm{1}}}{{\rm{x}}}} \right)^2} + {\left( {2y + \dfrac{1}{y}} \right)^2}\).

Phần I: Trắc nghiệm khách quan 

Bài 1:  Khoanh tròn vào chữ cái đứng trước câu trả lời đúng:

1) Giá trị của phân thức \(\dfrac{{4x{{(x - 2)}^2}}}{{{x^2} - 4}}\) tại x = -1 bằng:

A.  12

B. -12 

C.  \(\dfrac{1}{{12}}\)

D. \( - \dfrac{1}{{12}}\)

2) Điều kiện để giá trị phân thức \(\dfrac{{x + 1}}{{{x^3} - 2{x^2} + x}}\) được xác định là:

A.  \(x \ne 0\)

B.  \(x \ne 1\) 

C. \(x \ne 0\) và \(x \ne 1\)

D. \(x \ne 0\) và \(x \ne  - 1\)

3) Phương trình \(\dfrac{{{x^2} - 1}}{{x + 1}} = 1\) có nghiệm là:

A. -1

B. 2

C. 2 và -1

D. -2

4) Điều kiện xác định của phương trình:\(1 + \dfrac{x}{{3 - x}} = \dfrac{{5x}}{{(x + 2)(3 - x)}} + \dfrac{2}{{x + 2}}\) là:

A. \(x \ne 3\)

B. \(x \ne  - 2\)

C. \(x \ne 3\) và \(x \ne  - 2\)

D. \(x \ne 3\) hoặc \(x \ne  - 2\)

5) Nếu \(a \ge b\) thì \(10 - 2a\)…..\(10 - 2b\). Dấu thích hợp trong ô trống là:

A. <                            B. >

C. \( \le \)                            D. \( \ge \)

6) x= 1 là nghiệm của bất phương trình:

A. \(3x + 3 > 9\)

B. \( - 5x > 4x + 1\)

C. \(x - 2x <  - 2x + 4\) 

D. \(x - 6 > 5 - x\)

7) Cho hình lập phương có cạnh là 5 cm. Diện tích xung quanh của hình lập phương là:

A.  \(25c{m^2}\)                   B. \(125c{m^2}\)

C. \(150c{m^2}\)                   D. \(100c{m^2}\)

8) Cho hình hộp chữ nhật có chiều dài, chiều rộng, chiều cao lần lượt là: 5cm ; 3cm ; 2cm. Thể tích của hình hộp chữ nhật là:

A. \(54c{m^3}\)                    B. \(54c{m^2}\)

C. \(30c{m^2}\)                    D. \(30c{m^3}\)

Bài 2: Điền dấu “x” vào ô thích hợp:

Phần II: Tự luận 

Bài 1: Giải bất phương trình sau:

\(\dfrac{{1 - 2x}}{4} - 2 < \dfrac{{1 - 5x}}{8}\)

Bài 2:  Giải bài toán bằng cách lập phương trình:

Một đội máy kéo dự định mỗi ngày cày được 40 ha. Khi thực hiện, mỗi ngày cày được 52 ha. Vì vậy, đội không những đã cày xong trước thời hạn 2 ngày mà còn cày thêm được 4 ha nữa. Tính diện tích ruộng mà đội phải cày theo kế hoạch đã định?

Bài 3:  Cho \(\Delta \)ABC vuông tại A, đường cao AH (H\( \in \) BC). Biết BH = 4cm ; CH = 9cm. Gọi I, K lần lượt là hình chiếu của H lên AB và AC. Chứng minh rằng:

a) Tứ giác AIHK là hình chữ nhật.

b) Tam giác AKI  đồng dạng với tam giác ABC.      

c) Tính diện tích \(\Delta \)ABC.