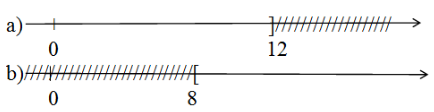Đọc hiểu - Đề số 46 - THPT

Trong các bất phương trình sau, hãy cho biết bất phương trình nào là bất phương trình bậc nhất một ẩn:

a) \(2x- 3 < 0\);

b) \(0.x + 5 > 0\);

c) \(5x - 15 ≥ 0\);

d) \({x^2}>0\)

Giải các bất phương trình sau:

a) \(x + 12 > 21\);

b) \(-2x > -3x - 5\).

Giải các bất phương trình sau (dùng quy tắc nhân):

a) \(2x < 24\);

b) \(-3x < 27\).

Giải thích sự tương đương:

a) \(x + 3 < 7 \Leftrightarrow x - 2 < 2\)

b) \(2x <  - 4 \Leftrightarrow  - 3x > 6\)

Giải bất phương trình \(- 4x - 8 < 0\) và biểu diễn tập nghiệm trên trục số.

Giải bất phương trình: \(-0,2x-0,2>0,4x-2\)

Giải các bất phương trình (theo quy tắc chuyển vế):

a) \(x - 5 > 3\);

b) \(x - 2x < -2x + 4\);

c) \(-3x > -4x + 2\);

d) \(8x + 2 < 7x - 1\).

Giải các bất phương trình (theo quy tắc nhân):

a) \(0,3x > 0,6\);              b) \(-4x < 12\);

c) \(-x > 4\);                     d) \(1,5x > -9\).

Giải thích sự tương đương sau:

a) \(x - 3 > 1 \Leftrightarrow x + 3 > 7\);

b) \(-x < 2 \Leftrightarrow  3x > -6\)

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) \(1,2x < -6\);

b) \(3x + 4 > 2x + 3\).

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) \(2x - 3 > 0\);                  b) \(3x + 4 < 0\);

c) \(4 - 3x ≤ 0\);                  d) \(5 - 2x ≥ 0\).

Giải các bất phương trình:

a) \(2x - 1 > 5\);               b) \(3x - 2 < 4\);

c) \(2 - 5x ≤ 17\);              d) \(3 - 4x ≥ 19\).

Giải các bất phương trình:

a) \( \dfrac{2}{3}x > -6\);             b) \( -\dfrac{5}{6}x < 20\);

c) \(3 -  \dfrac{1}{4}x > 2\);          d) \(5 - \dfrac{1}{3}x > 2\).

Hình vẽ sau biểu diễn tập nghiệm của bất phương trình nào? (kể cả bất phương trình có cùng tập nghiệm)

Đố. Kiểm tra xem giá trị \(x = -2\) có là nghiệm của bất phương trình sau không:

a) \(x + 2{x^2} - 3{x^3} + 4{x^4} - 5 < 2{x^2} \)\(\,- 3{x^3} + 4{x^4} - 6\)

b) \((-0,001)x > 0,003\).

Cho bất phương trình \({x^2} > 0\)

a) Chứng tỏ \(x = 2, x = -3\) là nghiệm của bất phương trình đã cho.

b) Có phải mọi giá trị của ẩn \(x\) đều là nghiệm của bất phương trình đã cho hay không?

Tìm \(x\) sao cho:

a) Giá trị của biểu thức \(2x - 5\) không âm;

b) Giá trị của biểu thức \(-3x\) không lớn hơn giá trị của biểu thức \(-7x + 5\).

Một người có số tiền không quá \(70 000\) đồng gồm \(15\) tờ giấy bạc với hai loại mệnh giá: loại \(2000\) đồng và loại \(5000\) đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại \(5000\) đồng?

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) \(\dfrac{{15 - 6x}}{3} > 5\)                                 

b) \(\dfrac{{8 - 11x}}{4} < 13\)

c) \(\dfrac{1}{4}\left( {x - 1} \right) < \dfrac{{x - 4}}{6}\)                                 

d) \(\dfrac{{2 - x}}{3} < \dfrac{{3 - 2x}}{5}\)

Giải các bất phương trình:

a) \(8x + 3(x + 1) > 5x - (2x - 6)\);

b) \(2x(6x - 1) > (3x - 2)(4x +3)\).

Đố: Trong một kì thi, bạn Chiến phải thi bốn môn Văn, Toán, Tiếng Anh và Hóa. Chiến đã thi ba môn và được kết quả như bảng sau:

Kì thi quy định muốn đạt loại giỏi phải có điểm trung bình các môn thi là 8 trở lên và không có môn nào bị điểm dưới 6. Biết môn Văn và Toán được tính hệ số 2. Hãy cho biết, để đạt loại giỏi bạn Chiến phải có điểm thi môn Toán ít nhất là bao nhiêu?

Tìm sai lầm trong các “lời giải” sau:

a) Giải bất phương trình \(-2x > 23\). Ta có:

\(-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25\).

Vậy nghiệm của bất phương trình là \(x > 25\).

b) Giải bất phương trình \(- \dfrac{3}{7}x > 12\) . Ta có:

 \( - \dfrac{3}{7}x > 12\)

\( \Leftrightarrow \left( { - \dfrac{7}{3}} \right).\left( { - \dfrac{3}{7}} \right) > \left( { - \dfrac{7}{3}} \right).12 \)

\(\Leftrightarrow x >  - 28\)

Vậy nghiệm của bất phương trình là \(x > -28\).