Đọc hiểu - Đề số 19 - THPT

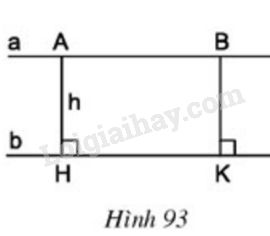
Cho hai đường thẳng song song \(a\) và \(b\) (h.\(93\)).

Gọi \(A\) và \(B \) là hai điểm bất kì thuộc đường thẳng \(a\), \(AH\) và \(BK\) là các đường vuông góc kẻ từ \(A\) và \(B\) đến đường thẳng \(b.\) Gọi độ dài \(AH\) là \(h.\) Tính độ dài \(BK\) theo \(h.\)

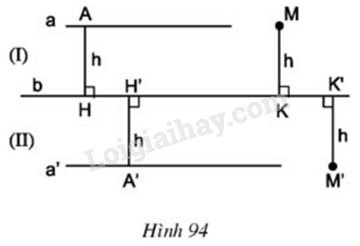
Cho đường thẳng \(b\). Gọi \(a\) và \(a’\) là hai đường thẳng song song với đường thẳng \(b\) và cùng cách đường thẳng \(b\) một khoảng bằng \(h \) (h.\(94\)), (I) và (II) là các nửa mặt phẳng bờ \(b.\) Gọi \(M, M’\) là các điểm cách đường thẳng \(b\) một khoảng bằng \(h\), trong đó \(M\) thuộc nửa mặt phẳng (I), \(M’\) thuộc nửa mặt phẳng (II). Chứng minh rằng \(M ∈ a, M’ ∈ a’.\)

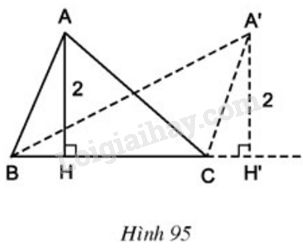
Xét các tam giác \(ABC\) có \(BC\) cố định, đường cao ứng với cạnh \(BC\) luôn bằng \(2 \,cm\) (h.\(95\)). Đỉnh \(A\) của các tam giác đó nằm trên đường nào?

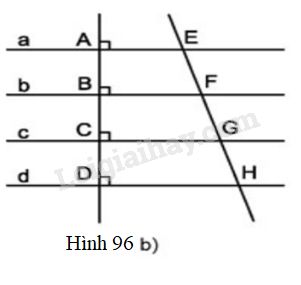
Cho hình \(96b\), trong đó các đường thẳng \(a, b, c, d\) song song với nhau.

Chứng minh rằng:

a) Nếu các đường thẳng \(a, b, c, d\) song song cách đều thì \(EF = FG = GH.\)

b) Nếu \(EF = FG = GH\) thì các đường thẳng \(a, b, c, d\) song song cách đều.

 Cho đoạn thẳng \(AB\). Kẻ tia \(Ax\) bất kì. Trên tia \(Ax\) lấy các điểm \(C, D, E\) sao cho \(AC = CD = DE\) (h.97). Kẻ đoạn thẳng \(EB\). Qua \(C, D\) kẻ các đường thẳng song song với \(EB\). Chứng minh rằng đoạn thẳng \(AB\) bị chia ra ba phần bằng nhau.

Cho điểm \(A\) nằm ngoài đường thẳng \(d\) và có khoảng cách đến \(d\) bằng \(2cm\). lấy điểm \(B\) bất kì thuộc đường thẳng \(d\). Gọi \(C\) là điểm đối xứng với điểm \(A\) qua điểm \(B\). Khi điểm \(B\) di chuyển trên đường thẳng \(d\) thì điểm \(C\) di chuyển trên đường nào ?

Ghép mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được một khẳng định đúng:

(1) Tập hợp các điểm cách điểm \(A\) cố định một khoảng \(3cm\)

(2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng \(AB\) cố định

(3) Tập hợp các điểm nằm trong góc \(xOy\) và cách đều hai cạnh của góc đó

(4) Tập hợp các điểm cách đều đường thẳng \(a\) cố định một khoảng \(3cm\)

(5) là đường trung trực của đoạn thẳng \(AB\).

(6) là hai đường thẳng song song với \(a\) và cách \(a\) một khoảng \(3cm\)

(7) là đường tròn tâm \(A\) bán kính \(3cm\).

(8) là tia phân giác của góc \(xOy\).

Cho góc vuông \(xOy\), điểm \(A\) thuộc tia \(Oy\) sao cho \(OA = 2cm\). Lấy \(B\) là một điểm bất kì thuộc tia \(Ox\). Gọi \(C\) là trung điểm của \(AB\). Khi điểm \(B\) di chuyển trên tia \(Ox\) thì điểm \(C\) di chuyển trên đường nào ?

Cho tam giác \(ABC\) vuông tại \(A\). Lấy \(M\) là một điểm bất kì thuộc cạnh \(BC\). Gọi \(MD\) là đường vuông góc kẻ từ \(M\) đến \(AB\), \(ME\) là đường vuông góc kẻ từ \(M\) đến \(AC\), \(O\) là trung điểm của \(DE\).

a) Chứng mình rằng ba điểm \(A, O, M\) thẳng hàng.

b) Khi điểm \(M\) di chuyển trên cạnh \(BC\) thì điểm \(O\) di chuyển trên đường nào ?

c) Điểm \(M\) ở vị trí nào trên cạnh \(BC\) thì \(AM\) có độ dài nhỏ nhất ?

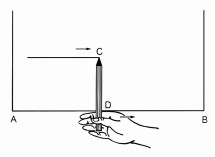
Đố. Để vạch một đường thẳng song song với mép gỗ \(10\,cm\), bác thợ mộc đặt đoạn bút chì \(CD\) dài \(10\,cm\) vuông góc với ngón tay trỏ lấy làm cữ (h.\(98\)), rồi đưa ngón trỏ chạy dọc theo mép gỗ \(AB.\) Căn cứ vào kiến thức nào mà ta kết luận được rằng đầu chì \(C\) vạch nên đường thẳng song song với \(AB\) và cách \(AB\) là \(10\,cm \)?

Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là chân đường vuông góc hạ từ H xuống AB và AC.

a) Chứng minh EF = AH.

b) Kẻ trung tuyến AM của tam giác ABC. Chứng minh \(AM \bot EF.\)

Cho tam giác ABC vuông tại A. Một đường thẳng d cắt hai cạnh AB, AC theo thứ tự tại các điểm D và E. Gọi I, J, K, H lần lượt là trung điểm của các đoạn thẳng DE, BE, BC, DC. Chứng minh IHKJ là hình bình chữ nhật.

Cho tam giác ABC có ba góc nhọn (AB < AC). Gọi AH là đường cao và M, N, P lần lượt là trung điểm cỉa AB, AC và BC. Gọi D là điểm đối xứng của H qua M.

a) Chứng minh tứ giác DAHB là hình chữ nhật.

b) Tìm điều kiện của \(\Delta ABC\(để AMPN là hình chữ nhật

Cho hình chữ nhật ABCD. Gọi H là chân đường vuông góc kẻ từ B xuống AC. Gọi M, N, P lần lượt là trung điểm của AB, AH và DC.

a)Chứng minh MBCP là hình chữ nhật.

b)Chứng minh \(BN \bot NP.\)

Cho tam giác ABC. Từ đỉnh A kẻ các đường thẳng AP, AQ theo thứ tự vuông góc với các tia phân giác trong và phân giác ngoài của góc B, các đường thẳng AR, AS theo thứ tự vuông góc với các ta phân giác trong và ngoài của góc C.

a) Chứng minh tứ giác APBQ là hình chữ nhật.

b) Chứng minh rằng 4 điểm Q, R, P, S thẳng hàng.

Cho hình bình hành ABCD. Phân giác các góc A, B, C, D cắt nhau tại các điểm M, N, P, Q. Chứng minh rằng tứ giác MNPQ là hình chữ nhật.

Tìm tập hợp (quỹ tích) các điểm cách đều hai đường thẳng song song cho trước.

Cho điểm A nằm ngoài đường thẳng d. Tìm tập hợp các trung điểm của đoạn thẳng AM khi M di chuyển trên đường thẳng d.

Cho tam giác ABC cân tại A, các điểm M, N theo thứ tự di động trên các cạnh AB và AC sao cho AM = CN. Hãy tìm tập hợp các trung điểm I của MN.

Cho hình chữ nhật ABCD. Gọi O là giao điểm của hai đường chéo AC và BD. Lấy E nằm giữa hai điểm O và B. Gọi F là điểm đối xứng với điểm A qua E và I là trung điểm của CF.

a) Chứng minh tứ giác OEFC là hình thang và tứ giác OEIC là hình bình hành.

b) Gọi H và K lần lượt là hình chiếu của điểm F trên các đường thẳng BC và CD. Chứng minh tứ giác CHFK là hình chữ nhật và I là trung điểm của đoạn HK.

c) Chứng minh ba điểm E, H, K thẳng hàng.