Đọc hiểu - Đề số 72 - THPT

Bài 1 (2 điểm)

1.Thực hiện phép tính:

a)\(2x\left( {{x^2} - 3y} \right)\)

b)\( - 18{x^3}{y^4}:3x{y^4}\)

2.Cho \(\Delta ABC\)có cạnh\(BC = 12cm\). Gọi\(M\)và\(N\)lần lượt là trung điểm của các cạnh\(AB,\,AC\) . Tính\(MN\).

Bài 2 (2 điểm)

1.Tìm\(x\), biết:

a)\({\left( {x + 2} \right)^2} - \left( {x - 2} \right)\left( {x + 2} \right) = 0\)

b)\(\left( {{x^2} - 2x + 1} \right):\left( {x - 1} \right) + 5x = 8\)

2.Phân tích đa thức sau thành nhân tử:

a.\(2{x^2} - 14x\)

b.\({x^2} - {y^2} + 5x + 5y\)

Bài 3 (2,0 điểm)Cho biểu thức:  \(A = \dfrac{{2{x^2}}}{{{x^2} - 1}} + \dfrac{x}{{x + 1}} - \dfrac{x}{{x - 1}}\)

a) Với giá trị nào của \(x\) thì giá trị của biểu thức\(A\)được xác định?

b)Rút gọn biểu thức \(A\).

c)Tìm các giá trị nguyên của\(x\)để biểu thức\(A\)có giá trị nguyên.

Bài 4 (3,5 điểm) Cho \(\Delta ABC\)vuông tại\(A\), đường cao \(AM\). Gọi \(D,\,E\) lần lượt là chân các đường vuông góc kẻ từ \(M\) đến các cạnh\(AB,\,AC\).

a)Tứ giác\(A{\rm{D}}ME\) là hình gì? Vì sao?

b)Chứng minh: \(AM.BC = AB.AC\)

c)Gọi\(I\)là trung điểm của\(MC\). Chứng minh rằng \(\Delta DEI\) vuông.

d) \(\Delta ABC\) phải có thêm điều kiện gì để \(DE = 2{\rm{E}}I\).

Bài 5 (0,5 điểm) Cho \(x,y\)thỏa mãn đẳng thức \(2{x^2} + 2{y^2} + 3xy - x + y + 1 = 0\). Tính giá trị của biểu thức \(P = {\left( {x + 2y} \right)^5} + {\left( {y + 1} \right)^4} + {\left( {x - 2} \right)^3}\).

Bài 1 (1,5 điểm)Phân tích các đa thức sau thành nhân tử:

\(a)\;\;3{a^3}{b^2} - 15{a^2}{b^3}\)

\(b)\;\;5{x^2} - 10x + 5 - 20{y^2}\)

Bài 2 (3 điểm)Thực hiện phép tính:

a) \(\left( {x - 3} \right)\left( {x - 6} \right) + x\left( {4 - x} \right)\)

b) \(\dfrac{{5x}}{{x - 1}} + \dfrac{{3x - 8}}{{x - 1}}\)\(\)

c) \({\left( {x + 4} \right)^2} - 25 + \left( {3 + x} \right)\left( {3 - x} \right)\)

d) \(\dfrac{{2x - 1}}{x} + \dfrac{{2x + 5}}{{4x - 3}} + \dfrac{{2{x^2} + x + 3}}{{3x - 4{x^2}}}\)

Bài 3 (1,5 điểm)

a) Thực hiện phép chia đa thức \(A = {x^3} - 7x + 3 - {x^2}\) cho đa thức \(B = x - 3\) .

b) Gọi Q là thương của phép chia A cho B. Chứng minh \(Q + 3\) luôn nhận giá trị dương với mọi \(x \ne 3.\)

Bài 4 (3 điểm)Cho \(\Delta ABC\)vuông tại A \(\left( {AB < AC} \right)\). Gọi \(M,\,N,K\) thứ tự là trung điểm của \(AB,\,AC\)  và \(BC\).

a)Chứng minh \(KN = \dfrac{1}{2}AB\)và \(ABKN\) là hình thang vuông.

b)Qua \(M\) kẻ đường thẳng song song với \(BN\), cắt tia \(KN\) tại \(Q\). Chứng minh \(AKCQ\) là hình thoi.

c)\(MN\) cắt \(BQ\) tại \(O\) , \(AK\) cắt \(BN\) tại \(I\). Biết \(BC = 24\,cm\). Tính độ dài \(OI\).

Bài 5 (1 điểm)Trong hình vẽ sau, hai địa điểm A và B cách nhau \(100\,km\). Một xe ô tô khởi hành từ B đến A với vận tốc \(40\,km/h\). Cùng lúc đó, một xe đạp điện cũng khởi hành từ A trên đoạn đường vuông góc với AB với vận tốc \(20\,km/h\). Gọi C, D thứ tự là vị trí của xe ô tô và xe đạp điện vào thời điểm t(h) sau khi khởi hành. Giả sử vận tốc của hai xe không thay đổi trong quá trình di chuyển.

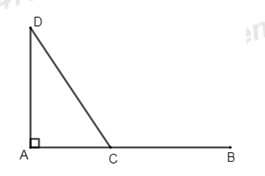
a)Viết biểu thức đại số biểu diễn độ dài \(AC,\,A{\rm{D}}\)  theo \(t\).

b)Hỏi sau bao lâu (tính từ lúc khởi hành) khoảng cách \(C{\rm{D}}\) là ngắn nhất? Giải thích.

Bài 1 (2 điểm)Phân tích các đa thức sau thành nhân tử:

a)\(2{x^3} - 50x\)

b)\({x^2} - 6x + 9 - 4{y^2}\)

c)\({x^2} - 7x + 10\)

Bài 2 (1,5 điểm)

a.Làm tính chia: \(\left( {12{x^6}{y^4} + 9{x^5}{y^3} - 15{x^2}{y^3}} \right):3{x^2}{y^3}\)

b. Rút gọn biểu thức: \(\left( {{x^2} - 2} \right)\left( {1 - x} \right) + \left( {x + 3} \right)\left( {{x^2} - 3x + 9} \right)\)

Bài 3 (2,5 điểm)Cho biểu thức: \(A = \dfrac{5}{{x + 3}} - \dfrac{2}{{3 - x}} - \dfrac{{3{x^2} - 2x - 9}}{{{x^2} - 9}}\) (với \(x \ne  \pm 3\))

a)Rút gọn biểu thức \(A\).

b)Tính giá trị của \(A\) khi \(\left| {x - 2} \right| = 1\)

c)Tìm giá trị nguyên của \(x\) để\(A\) có giá trị nguyên.

Bài 4 (3,5 điểm)Cho \(\Delta ABC\)vuông tại \(A\), gọi \(M\) là trung điểm của \(AC\). Gọi \(D\) là điểm đối xứng với \(B\)  qua \(M\).

a)Chứng minh tứ giác \(ABC{\rm{D}}\) là hình bình hành.

b)Gọi \(N\) là điểm đối xứng với \(B\)  qua \(A\). Chứng minh tứ giác \(AC{\rm{D}}N\) là hình chữ nhật.

c)Kéo dài \(MN\) cắt \(BC\) tại \(I\). Vẽ đường thẳng qua \(A\) song song với \(MN\) cắt \(BC\) ở\(K\). Chứng minh: \(KC = 2BK\)

d)Qua \(B\) kẻ đường thẳng song song với \(MN\) cắt \(AC\) kéo dài tại \(E\) . Tam giác \(ABC\) cần có thêm điều kiện gì để tứ giác \(EBMN\) là hình vuông.

Bài 5 (0,5 điểm)Cho \(a\) thỏa mãn: \({a^2} - 5a + 2 = 0\). Tính giá trị của biểu thức:\(P = {a^5} - {a^4} - 18{a^3} + 9{a^2} - 5a + 2017 + \left( {{a^4} - 40{a^2} + 4} \right):{a^2}\)

\(\begin{array}{l}P = \dfrac{{{a^4} + 1975{a^2} + 4}}{{{a^2}}}\\\;\;\; = \dfrac{{\left( {{a^4} - 10{{\rm{a}}^3} + 25{{\rm{a}}^2}} \right) + \left( {10{a^3} - 50{a^2} + 20a} \right) + \left( {4{a^2} - 20a + 8} \right) + 1996{a^2} - 4}}{{{a^2}}}\\\;\;\; = \dfrac{{4 + 10a\left( {{a^2} - 5a + 2} \right) + 4\left( {{a^2} - 5a + 2} \right) + 1996{a^2} - 4}}{{{a^2}}} = 1996\end{array}\)

Vậy \(P = 1996.\)

Bài 1 (2 điểm)

a) Phân tích đa thức sau thành nhân tử: \(x\left( {x - y} \right) + 2\left( {x - y} \right)\)

b) Tính nhanh giá trị của biểu thức: \({x^2} - 6{\rm{x}}y + 9{y^2}\) tại \(x = 16,\,y = 2\)

c) Tìm x, biết: \(2x\left( {x - 5} \right) - x\left( {2x + 3} \right) = 26\)

Bài 2 (2 điểm)

a) Rút gọn biểu thức: \(\dfrac{{{x^2} + xy}}{{{x^2} - {y^2}}}\)

b) Thực hiện phép tính: \(\dfrac{{4x + 12}}{{{{\left( {x + 1} \right)}^2}}}:\dfrac{{3\left( {x + 3} \right)}}{{x + 1}}\)

c) Thực hiện phép tính: \(\dfrac{4}{{x + 2}} + \dfrac{3}{{x - 2}} + \dfrac{{ - 5x - 2}}{{{x^2} - 4}}\)

Bài 3 (1,5 điểm)Cho hai đa thức \(A = 2{x^2} + 3x + 3\) và \(B = 2x - 1\).

a) Thực hiện phép chia A cho B.

b) Tìm các giá trị nguyên của x để giá trị của đa thức A chia hết cho giá trị của đa thức B.

Bài 4 (4 điểm)Cho \(\Delta ABC\) cân tại A. Gọi \(H,\,K\) lần lượt là trung điểm của \(BC\)  và \(AC\).

a)Chứng minh tứ giác \(ABHK\) là hình thang.

b)Trên tia đối của tia \(HA\) lấy điểm \(E\)  sao cho \(H\) là trung điểm của cạnh \(A{\rm{E}}\). Chứng minh tứ giác \(ABEC\) là hình thoi.

c) Qua A vẽ đường thẳng vuông góc với \(AH\) cắt tia \(HK\) tại \(D\). Chứng minh \(A{\rm{D}} = BH\).

d) Vẽ \(HN \bot AB\left( {N \in AB} \right)\), gọi I là trung điểm của AN. Trên tia đối của tia BH lấy điểm M sao cho B là trung điểm của HM. Chứng minh: \(MN \bot HI\)

Bài 5 (0,5 điểm)

Cho \(x,y,z\) là ba số thỏa mãn điều kiện: \(4{x^2} + 2{y^2} + 2{{\rm{z}}^2} - 4xy - 4x{\rm{z}} + 2yz - 6y - 10{\rm{z}} + 34 = 0\)

Tính: \(S = {\left( {x - 4} \right)^{2017}} + {\left( {y - 4} \right)^{2017}} + {\left( {z - 4} \right)^{2017}}\)

Bài 1  (1 điểm)Chọn đáp án đúng nhất.

1.Thu gọn biểu thức: \({\left( {x + y} \right)^2} - {\left( {x - y} \right)^2}\) được kết quả là:

A.\(2x\)

B.\(2y\)

C.\(2xy\)

D.\(4xy\)

2. Giá trị của phân thức: \(\dfrac{{x + 2}}{{{x^2} - 4}}\) không xác định tại các giá trị của biến \(x\) là:

A.\(x \ne  \pm 2\)

B.\(x \ne 2\)

C.\(x =  \pm 2\)

D.\(x = 2\)

3. Tam giác vuông cân có độ dài đường trung tuyến ứng với cạnh huyền bằng \(\sqrt 2 \,cm\) thì độ dài cạnh góc vuông của tam giác đó bằng:….

 4) Xét 4 khẳng định sau: 

a)      Biểu thức \({x^2} + ax + 4\) là bình phương của một tổng khi \(a = 2\).

b)      Dư trong phép chia đa thức\({y^3} - {y^2} + 3y - 2\)  cho đa thức\({y^2} + 1\)  là\(2y - 1\).

c)      Hình thang có hai góc bằng nhau là hình thang cân.

d)     Hai đỉnh \(M\)  và \(P\) của hình thoi \(MNPQ\) đối xứng với nhau qua đường thẳng \(NQ\).

Trong 4 khẳng định trên, có bao nhiêu khẳng định đúng?

A.    Một

B.     Hai

C.    Ba

D.    Bốn

Bài 2 (3 điểm)

1.Phân tích đa thức thành nhân tử:

a)\(3{x^2} - 6x + 2xy - 4y\)

b)\({a^2}\left( {{a^2} + 4} \right) - {a^2} + 4\)

2.Tìm \(x\) biết: \({x^2} - x + 0,25 = 0.\)

3.Chứng minh giá trị biểu thức  \({\left( {m - 1} \right)^3} - \left( {{m^2} + 1} \right)\left( {m - 3} \right) - 2m\) là số nguyên tố với mọi giá trị của \(m\).

Bài 3 (2,5 điểm)

\(\left( {\dfrac{x}{{2 + x}} - \dfrac{1}{{x - 2}} - \dfrac{{x + 3}}{{4 - {x^2}}}} \right):\left( {\dfrac{{{x^2} - 3}}{{4 - {x^2}}} + 1} \right) =  - {\left( {x - 1} \right)^2}\)

Bài 4 (1,5 điểm)Cho \(\Delta ABC\) vuông tại \(A\) , có \(D\) là trung điểm của \(BC\). Gọi \(E,\,F\) lần lượt là hình chiếu của \(D\)  trên \(AB\)  và \(AC\).

Bài 5  (1 điểm)

Bài 1 (2 điểm)Chọn chữ cái trước đáp án đúng:

1.      Đa thức \(12x - 36 - {x^2}\) bằng:

A.    \( - {\left( {x + 6} \right)^2}\)

B.     \({\left( { - x - 6} \right)^2}\)

C.    \({\left( { - x + 6} \right)^2}\)

D.    \( - {\left( {x - 6} \right)^2}\)

2.      Kết quả của phép cộng: \(\dfrac{{3x - 1}}{{3x - 3}} + \dfrac{{ - 2}}{{3x - 3}}\)là:

A.    \(\dfrac{{3x + 1}}{{3x - 3}}\)

B.     \(\dfrac{{x + 1}}{{x - 3}}\)

C.    \(1\)

D.    \(\dfrac{{3x - 5}}{{3\left( {3x - 3} \right)}}\)

3.      Kết quả rút gọn biểu thức:\(\left( {x - 2y} \right)\left( {{x^2} + 2xy + 4{y^2}} \right) - \left( {x + 2y} \right)\left( {{x^2} - 2xy + 4{y^2}} \right)\) là:

A.    \( - 16{y^3}\)

B.     \( - 4{y^3}\)

C.    \(16{y^3}\)

D.    \( - 12{y^3}\)

4.      Số dư khi chia đa thức: \(3{x^4} - 2{x^3} + {x^2} - 2x + 2\) cho đa thức \(x - 2\) là:

A.    \(50\)

B.     \(34\)

C.    \(32\)

D.    \(30\)

5.      Hình vuông có độ dài đường chéo là \(6cm\). Độ dài cạnh hình vuông đó là:

A.    \(\sqrt {18} \,cm\)

B.     \(18\,cm\)

C.    \(3\,cm\)

D.    \(4\,cm\)

6.      Một hình chữ nhật có diện tích \(15{m^2}\). Nếu tăng chiều dài lên hai lần, chiều rộng lên ba lần thì diện tích của hình chữ nhật mới là:

A.    \(30\,{m^2}\)

B.     \(45\,{m^2}\)

C.    \(90\,{m^2}\)

D.    \(75\,{m^2}\)

7.      Cho hình thang cân \(ABC{\rm{D}}\,\left( {AB//C{\rm{D}}} \right)\) có \(\angle A = {135^0}\) thì \(\angle C\) bằng:

A.    \({35^0}\)

B.     \({45^0}\)

C.    \({55^0}\)

D.    Không tính được.

8.      Tứ giác có các đỉnh là trung điểm các cạnh của một tứ giác có hai đường chéo bằng nhau là:

A.    Hình thang cân

B.     Hình chữ nhật

C.    Hình thoi

D.    Hình vuông

Bài 2 (1,0 điểm)Phân tích đa thức sau thành nhân tử:

a)\(6xy + 12x - 4y - 8\)

b)\({x^3} + 2{x^2} - x - 2\)

Bài 3 (1,5 điểm)

a)Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biểu thức: \({\left( {x - 2} \right)^2} - \left( {x - 1} \right)\left( {x + 1} \right) + 4\left( {x + 2} \right)\)

b)Tìm \(x\) biết: \(\left( {2 - x} \right)\left( {2 + x} \right) = 3\)

Bài 4 Thực hiện phép tính:

a)\(\dfrac{{x + 2}}{{x - 3}} - \dfrac{{{x^2} + 6}}{{{x^2} - 3x}}\)

b)\(\dfrac{{4x - 4}}{{{x^2} - 4x + 4}}:\dfrac{{{x^2} - 1}}{{{{\left( {2 - x} \right)}^2}}}\)

Bài 5 Cho \(\Delta ABC\) có \(A{\rm{D}}\) là phân giác của \(\angle BAC\;\,\,\left( {D \in BC} \right)\). Từ\(D\) kẻ các đường thẳng song song với \(AB\)  và \(AC\), chúng cắt \(AC,\,AB\) tại \(E\)  và \(F\).

a)Chứng minh: Tứ giác \(A{\rm{ED}}F\) là hình thoi.

b)Trên tia \(AB\) lấy điểm \(G\)  sao cho \(F\) là trung điểm \(AG\). Chứng minh: Tứ giác \(EFG{\rm{D}}\) là hình bình hành.

c)Gọi \(I\) là điểm đối xứng của \(D\)  qua \(F\) , tia \(IA\) cắt tia \(DE\) tại \(K\). Gọi \(O\) là giao điểm của \(A{\rm{D}}\)  và \(EF\). Chứng minh: \(G\) đối xứng với \(K\)  qua \(O\).

d)Tìm điều kiện của \(\Delta ABC\)để tứ giác \(A{\rm{D}}GI\) là hình vuông.

Bài 6 : Tính giá trị của biểu thức:\(\left( {1 - \dfrac{1}{{{2^2}}}} \right)\left( {1 - \dfrac{1}{{{3^2}}}} \right)\left( {1 - \dfrac{1}{{{4^2}}}} \right)...\left( {1 - \dfrac{1}{{{{2017}^2}}}} \right)\)

Bài 1 (2 điểm)Phân tích các đa thức sau thành nhân tử:

a)\(2{x^3}y - 50xy\)

b)\({x^2} - 6x - 4{y^2} + 9\)

Bài 2 (1 điểm)Thực hiện phép tính:

a)\(\left( {x - 3} \right)\left( {{x^2} + 4x + 5} \right)\)

b)\(\left( {2{x^3} - 4{x^2} - 5x + 7} \right):\left( {x - 1} \right)\)

Bài 3 (2,5 điểm)Tìm số thực\(x\), biết:

a)\(2{x^3} - 2{x^2} + 2017x - 2017 = 0\)

b)\(2{x^2} + 4x = 0\)

Bài 4 (2,5 điểm)Cho biểu thức \(A = \dfrac{{{x^2}}}{{{x^2} - 4}} - \dfrac{x}{{x - 2}} + \dfrac{2}{{x + 2}}\)

a)Tìm điều kiện của \(x\) để biểu thức xác định.

b)Rút gọn biểu thức A.

c)Tính giá trị của biểu thức A khi \(\left| {2x - 1} \right| = 1\).

Bài 5 (4 điểm)Cho \(\Delta MNP\) vuông tại \(M\), đường cao \(MH\). Biết \(MN = 3cm,\,NP = 5cm\). Gọi \(D,\,\,E\) lần lượt là chân các đường vuông góc hạ từ\(H\) xuống \(MN\)  và \(MP\).

a)Tính diện tích \(\Delta MNP\).

b)Chứng minh tứ giác \(M{\rm{D}}HE\) là hình chữ nhật.

c)Tính độ dài đoạn \(DE\).

d)Gọi \(A\) là trung điển của \(HP\). Tính \(\angle DE{\rm{A}}\).

Bài 6 (0,5 điểm)Cho \(a + b = 1\). Tính giá trị của biểu thức:

\(S = {a^3} + {b^3} + 3ab\left( {{a^2} + {b^2}} \right) + 6{a^2}{b^2}\left( {a + b} \right)\)

Bài 1 (1,5 điểm)

1.Tính: \(\dfrac{1}{5}{x^2}y\left( {15x{y^2} - 5y + 3xy} \right).\)

2.Phân tích các đa thức sau thành nhân tử:

a)\(5{x^3} - 5x\)

b)\(3{x^2} + 5y - 3xy - 5x\)

Bài 2 (2,0 điểm)Cho \(P = \left( {\dfrac{{x + 2}}{{2x - 4}} + \dfrac{{x - 2}}{{2x{\rm{ + }}4}} + \dfrac{{ - 8}}{{{x^2} - 4}}} \right):\dfrac{4}{{x - 2}}\)

a)Tìm điều kiện của \(x\) để P xác định.

b)Rút gọn biểu thức P.

c)Tính giá trị của biểu thức P khi \(x =  - 1\dfrac{1}{3}\)

Bài 3 (2,0 điểm)Cho hai đa thức \(A = 2{x^3} + 5{x^2} - 2x + a\) và \(B = 2{x^2} - x + 1\).

a)Tính giá trị đa thức \(B\) tại \(x =  - 1\)

b)Tìm \(a\) để đa thức \(A\) chia hết cho đa thức \(B\).

c)Tìm \(x\)để giá trị đa thức \(B = 1\).

Bài 4 (3,5 điểm)Cho \(\Delta ABC\)có \(\angle A = {90^0}\) và \(AH\) là đường cao. Gọi\(D\) là điểm đối xứng với \(H\)  qua \(AB,\,E\) là điểm đối xứng với \(H\)  qua \(AC\). Gọi \(I\) là giao điểm của \(AB\)  và \(DH,\,K\) là giao điểm của \(AC\)  và \(HE\).

a)Tứ giác \(AIHK\) là hình gì? Vì sao?

b)Chứng minh ba điểm \(D,\,A,\,E\) thẳng hàng.

c)Chứng minh: \(CB = B{\rm{D}} + CE\)

d)Biết diện tích tứ giác \(AIHK\) là \(a\)(đvdt). Tính diện tích \(\Delta DHE\) theo \(a\).

Bài 5 (1,0 điểm)

a)Tìm các số\(x,\,y\) thỏa mãn đẳng thức: \(3{x^2} + 3{y^2} + 4xy + 2x - 2y + 2 = 0\)

b)Với \(a,\,b,\,c,\,d\) dương, chứng minh: \(F = \dfrac{a}{{b + c}} + \dfrac{b}{{c + d}} + \dfrac{c}{{d + a}} + \dfrac{d}{{a + b}} \ge 2\)

I. TRẮC NGHIỆM (2 điểm)

Câu 1 : Phân thức: \(\dfrac{{{x^2} - 2017}}{{1 + {x^{2018}}}}\) xác định với:

A. \(x \ne 1\)                         B. \(x \ne  - 1\)

C.\(x \ne 0\)                          D.\(\forall x \in R\)

Câu 2 : Biểu thức P trong đẳng thức: \(\dfrac{{4{x^2} - 16}}{{2x + {x^2}}} = \dfrac{P}{x}\) là:

A.\(\dfrac{{4x - 8}}{x}\)               B. \(4x - 8\)

C.\(2x - 4\)               D.\(2x - 2\)

Câu 3 : Hình vuông có đường chéo bằng \(2\,dm\) thì cạnh bằng:

A. \(\dfrac{3}{2}\,dm\)                                   B. \(1\,dm\)

C.\(\sqrt 2 \,dm\)                                D.\(2\,dm\)

Câu 4 :  Hình thoi có hai đường chéo bằng \(6\,cm\)và \(8\,cm\)thì cạnh bằng:

A. \(5\,cm\)                           B. \(10\,cm\)

C.\(12,5\,cm\)                        D.\(7\,cm\)

II. TỰ LUẬN (8 điểm)

Bài 1  Phân tích đa thức thành nhân tử:

a)\({x^2} + 2x\)

b)\({x^3} - 5{x^2} + 5x - 1\)

Bài 2 Thực hiện phép tính:

a)\(\left( {{x^3} + {x^2} - 3x + 9} \right):\left( {x + 3} \right)\)

b)\(\dfrac{{4x - 8}}{{x + 5}}:\dfrac{{25 - {x^2}}}{{2x - {x^2}}}\)

Bài 3 (2,0 điểm)Cho biểu thức: \(A = \dfrac{1}{{x + 1}} + \dfrac{{x - 1}}{x} + \dfrac{{x + 2}}{{{x^2} + x}}\)

a)Tìm giá trị của \(x\)để giá trị của biểu thức A xác định.

b)Rút gọn A.

Bài 4 Cho hình vuông \(ABC{\rm{D}}\). Trên các cạnh \(AB,\,BC,\,C{\rm{D}},\,DA\) lần lượt lấy các điểm \(M,\,N,\,E,\,F\) sao cho \(AM = CN = CE = AF\).

a)Chứng minh tứ giác \(ANCF\) là hình bình hành.

b)Chứng minh tứ giác \(MNEF\) là hình chữ nhật.

c)Gọi \(H\) là hình chiếu của \(A\)  trên \(BF\). Tính \(\angle CHM\).

Bài 5 : Cho \(x + y = 2\) chứng minh: \({x^{2017}} + {y^{2017}} \le {x^{2018}} + {y^{2018}}\)

I.  TRẮC NGHIỆM (2 điểm)

Câu 1 :Kết quả của phép tính: \(\left( {{a^2} + 2a + 4} \right)\left( {a - 2} \right)\) là:

A.    \({a^3} - 8\)

B.     \({\left( {a - 2} \right)^3}\)

C.    \({a^3} + 8\)

D.    \({\left( {a + 2} \right)^3}\)

Câu 2 : Kết quả của phép tính: \(\left( { - 2017{x^4}{y^3}} \right):\left( { - {x^3}{y^3}} \right)\) là:

A.    \( - 2017x\)

B.     \(2017x\)

C.    \( - 2017xy\)

D.    \(2017xy\)

Câu 3 : Phân tích đa thức \({x^2} - x - 6\) thành nhân tử được kết quả là:

A.\(\left( {x + 2} \right)\left( {x + 3} \right)\)

B.\(\left( {x - 2} \right)\left( {x + 3} \right)\)

C.\(\left( {x - 2} \right)\left( {x - 3} \right)\)

D.\(\left( {x + 2} \right)\left( {x - 3} \right)\)

Câu 4 : Tập hợp tất cả các giá trị của \(x\) thỏa mãn: \({x^3} =  - x\) là:

A.    \(\left\{ {0;\, - 1} \right\}\)

B.     \(\emptyset \)

C.    \(\left\{ 0 \right\}\)

D.    \(\left\{ {0; \pm 1} \right\}\)

Câu 5 : Hình chữ nhật \(ABC{\rm{D}}\) có \(AB = 6\,cm,\,BC = 4\,cm\). Khi đó, diện tích hình chữ nhật ABCD là:

A.    \(2\,c{m^2}\)

B.     \(10\,c{m^2}\)

C.    \(12\,c{m^2}\)

D.    \(24\,c{m^2}\)

Câu 6 : Số lượng trục đối xứng của hình vuông là:

A.    \(6\)

B.     \(4\)

C.    \(2\)

D.    \(1\)

Câu 7 : Một hình thoi có cạnh bằng \(10\,cm\)và độ dài một đường chéo là \(12\,cm\). Khi đó, độ dài đường chéo còn lại của hình thoi là:

A.    \(16\,cm\)

B.     \(12\,cm\)

C.    \(8\,cm\)

D.    \(4cm\)

Câu 8 : Tứ giác là hình vuông khi tứ giác đó có:

A.    Hai đường chéo bằng nhau và vuông góc với nhau

B.     Bốn cạnh bằng nhau

C.    Bốn cạnh bằng nhau và có một góc vuông

D.    Bốn góc vuông.

II. TỰ LUẬN (8 điểm)

Bài 1 (1,5 điểm)Phân tích các đa thức sau thành nhân tử:

a)\(2x - 4{x^2}\)

b)\(3x\left( {x - 2} \right) - 4x + 8\)

c)\({x^2} - 2xy + {y^2} - 9{{\rm{z}}^2}\)

Bài 2 (1,25 điểm)

a)Tìm số\(m\), biết đa thức \(2{x^3} - 3{x^2} + x + m\)chia hết cho đa thức \(x + 2\)

b)Cho \(P = x - {x^2} - 1\), chứng minh \(P < 0\,\forall \,x\)

Bài 3 (1,25 điểm)Rút gọn các phân thức sau:

a)\(A = \dfrac{{45x\left( {2 - x} \right)}}{{15x{{\left( {x - 2} \right)}^2}}}\)

b)\(B = \dfrac{{{x^3} + 2{x^2}y - x{y^2} - 2{y^3}}}{{{x^2} + 3xy + 2{y^2}}}\)

Bài 4 (3,0 điểm)Cho \(\Delta ABC\) vuông tại \(A\), đường cao \(AH\). Gọi \(M,\,N\) theo thứ tự là chân các đường vuông góc kẻ từ\(H\) đến \(AB,\,AC\). Gọi \(O\) là giao điểm của \(AH\)  và \(MN\),\(K\)là trung điểm của \(CH\)

a)Chứng minh rằng tứ giác \(AMHN\) là hình chữ nhật.

b)Tính số đo \(\angle MNK\)

c)Chứng minh rằng \(BO \bot AK\)

Bài 5 (1,0 điểm)Chứng minh: \({a^4} + {b^4} + {c^4} = 2{\left( {ab + bc + ac} \right)^2}\). Biết rằng \(a + b + c = 0\)

PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (2 điểm)

Lựa chọn chữ cái đứng trước câu trả lời đúng

Câu 1 : Kết quả của phép tính \(8{x^2}:4x\) là:

A.\(2\)                                      B.\( - 2x\)        

C.\(2x\)                                    D.\( - 2\)

Câu 2 : Biểu thức \({x^2} - {y^2}\) bằng:

A.\((x + y)(x + y)\)

B.\((x - y)(x + y)\)

C.\({x^2} + 2xy + {y^2}\)

D.\({x^2} - 2xy + {y^2}\)

Câu 3 : Phân tích đa thức \(x{y^2} + 2xy + x\) ta được:

A.\(x(x + 1)\)               B.\(x{(y + 1)^2}\)

C.\((x - 1)(x + y)\)       D.\(y{(x + 1)^2}\)

Câu 4 : Tổng của hai phân thức \(\dfrac{3}{{7xy}} + \dfrac{4}{{7xy}}\) là

A.\(\dfrac{1}{{xy}}\)                          B.\(\dfrac{3}{{xy}}\)

C.\(\dfrac{4}{{xy}}\)                          D.\(\dfrac{7}{{xy}}\)

Câu 5 : Hình nào sau đây không có tâm đối xứng?

A.Hình bình hành

B.Hình chữ nhật                                

C.Hình thang cân

D.Cả ba hình trên

Câu 6 : Hình thang cân là:

A.Hình thang có hai góc kề một đáy bằng nhau.

B.Tứ giác có các cạnh đối song song 

C.Hình thang có hai cạnh bên bằng nhau

D.Hình thang có hai đường chéo bằng nhau

Câu 7 : Cho tam giác vuông như hình vẽ:

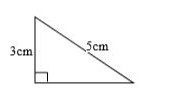
Diện tích của tam giác bằng:

A.\(7c{m^2}\)                         B.\(6c{m^2}\)

C.\(8c{m^2}\)                         D.\(4c{m^2}\)

PHẦN II. TỰ LUẬN (8 điểm)

Câu 8 (2 điểm):Thực hiện phép tính:

\(a)\,\,2x.(3{x^2} + 1)\\b)\,\,\left( {2{x^3} - 5{x^2} + 6x} \right):2x\)

Câu 9 (1 điểm):

a) Tìm \(x\) biết: \({x^2} + 5x = 0\) .

b) Phân tích đa thức sau thành nhân tử:  \({x^2} - 2x - xy + 2y\).

Câu 10 (2 điểm):Cho \(Q = \dfrac{{2(x - 2)}}{{6(x - 2)}}\)

a) Tìm điều kiện xác định của \(Q\).

b) Thu gọn biểu thức \(Q\).

Câu 11 (2 điểm):Một mảnh vườn lúc đầu có dạng tam giác \(ABC\) vuông tại \(A\), bờ rào \(AB\) dài \(5m\), rào \(AC\) dài \(12m\). Người ta sử dụng lưới ngăn dọc theo hai điểm \(E,\,\,M\)(\(E\) là trung điểm của \(AC\) và \(M\) là trung điểm của \(BC\)) để chia mảnh vườn thành hai phần trồng rau và hoa.

a) Tính độ dài của lưới \(ME\) phải dùng.

b) Mảnh vườn \(AEMB\) là hình gì? Vì sao?

c) Tính diện tích mảnh vườn \(AEMB\).

Câu 12 (1 điểm):

a) Tìm giá trị nhỏ nhất của \(A = {x^2} - 2x + 3\) với mọi số thực \(x \in Z\).

b) Tìm giá trị nguyên của \(n\) để \(({n^3} - 3{n^2} + n)\,\, \vdots \,\,(n - 3)\).

Câu 1 (2,0 điểm):

1) Rút gọn rồi tính giá trịbiểu thức: \((2x + y)(y - 2x) + 4{x^2}\) tại \(x =  - 2018\) và \(y = 10\).

2) Phân tích các đa thức sau thành nhân tử:

\(a)\,\,xy + 11x\\b)\,\,{x^2} + 4{y^2} + 4xy - 16\)

Câu 2 (2,0 điểm):

1)Tìm \(x\) biết:

\(a)\,\,2{x^2} - 6x = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b)\,\,(x + 3)({x^2} - 3x + 9) - x({x^2} - 2) = 15\)

2) Tìm số nguyên \(a\) sao cho \({x^3} + 3{x^2} - 8x + a - 2038\) chia hết cho \(x + 2\).

Câu 3 (2,0 điểm):Rút gọn các biểu thức sau:

\(\begin{array}{l}1)\,\,\dfrac{{6x + 4}}{{3x}}:\dfrac{{2y}}{{3x}}\\2)\,\,A = \left( {\dfrac{{x - 3}}{x} - \dfrac{x}{{x - 3}} + \dfrac{9}{{{x^2} - 3x}}} \right):\dfrac{{2x - 2}}{x}\end{array}\)

Câu 4 (3,0 điểm):Cho tam giác \(ABC,\,\,M,\,\,N\) lần lượt là trung điểm của \(AB\) và \(AC\). Gọi \(D\) là điểm đối xứng với điểm \(M\) qua điểm \(N\).

a) Tứ giác \(AMCD\) là hình gì? Vì sao?

Tìm điều kiện của tam giác \(ABC\) để tứ giác \(AMCD\) là hình chữ nhật.

b) Chứng minh tứ giác \(BCDM\) là hình bình hành.

Câu 5 (1,0 điểm):

a)  Cho \(x,y\) thỏa mãn \(2{x^2} + {y^2} + 9 = 6x + 2xy\). Tính giá trị của biểu thức \(A = {x^{2017}}{y^{2018}} - {x^{2018}}{y^{2017}} + \dfrac{1}{9}xy\).

b) Cho \(2\) số \(a\) và \(b\) thỏa mãn \(\dfrac{{a + b}}{2} = 1\).Tính giá trị lớn nhất của biểu thức: \(\dfrac{{2011}}{{2{a^2} + 2{b^2} + 2008}}\) .

I. Phần trắc nghiệm (2 điểm): Hãy chọn đáp án đúng trong các câu sau:

Câu 1 : Phép nhân \(5x(3{x^2} - 4x + 2)\) được kết quả là

A.\(15{x^3} - 20{x^2} + 2\)

B.\(15{x^3} + 20{x^2} + 10x\)

C.\(15{x^3} - 20{x^2} + 10x\)

D.\(15{x^3} - 4x + 2\)

Câu 2 : Thực hiện phép chia \(\left( {{x^2} + 2017x} \right):\left( {x + 2017} \right)\) ta được kết quả là:

A.\(x\)                                      B.\(2x\)

C.\(2\)                                      D.\(2 + x\)

Câu 3 : Chọn câu phát biểu sai?

A.Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.               

B.Hình vuông là hình có trục đối xứng và có tâm đối xứng.                         

C.Hình thoi có một góc vuông là hình vuông.                      

D. Hình thang có hai cạnh bên bằng nhau là hình thang cân.

Câu 4 : Nếu tăng độ dài của một hình vuông lên \(3\)lần thì diện tích hình vuông đó tăng lên mấy lần?

A.\(3\)lần                                 B.\(6\)lần        

C.\(9\)lần                                 D.\(12\)lần

II. Phần tự luận (8 điểm):

Câu 5 .

a) Tính giá trị của biểu thức \(B = {x^2} + 2x + 1 + {y^2} - 4y + 4\) tại \(x = 99\) và \(y = 102\).

b) Phân tích đa thức sau thành nhân tử: \(2{x^2} - 2{y^2} + 16x + 32\).

c) Tìm \(x\) biết: \({x^2} - 3x + 2x - 6 = 0\).

Câu 6 .

a) Rút gọn phân thức: \(P = \dfrac{{9 - {x^2}}}{{{x^2} - 3x}}\).

b) Thực hiện phép tính: \(\dfrac{{{x^2}}}{{{x^2} + 2x + 1}} - \dfrac{1}{{{x^2} + 2x + 1}} + \dfrac{2}{{x + 1}}\).

Câu 7 .

Cho tam giác \(ABC\) vuông tại \(A\). Trên cạnh \(BC\) lấy điểm \(M\) bất kì. Gọi \(D,E\) lần lượt là chân đường vuông góc kẻ từ \(M\) xuống cạnh \(AB\) và \(AC\).

a) Tứ giác \(ADME\) là hình gì? Vì sao?

b) Điểm \(M\) ở vị trí nào trên cạnh \(BC\) để tứ giác \(ADME\) là hình vuông?

c) Gọi \(I\) là trung điểm đoạn thẳng \(BM\) và \(K\) là trung điểm đoạn thẳng \(CM\)và tứ giác \(DEKI\) là hình bình hành. Chứng minh rằng \(DE\) là đường trung bình của tam giác \(ABC\).

Câu 8 .

a) Tìm giá trị nhỏ nhất của biểu thức: \(P = {x^4} + {x^2} - 6x + 9\).

b) Chứng minh rằng \({n^2} + 11n + 39\) không chia hết cho \(49\) với mọi số tự nhiên \(n\) .

A. TRẮC NGHIỆM (2,0 điểm)

Câu 1 : (1,0 điểm) Chọn phương án trả lời đúng cho các câu sau:

1. Kết quả rút gọn của \(\dfrac{{ - 4{x^2} - 4x}}{{1 - {x^2}}}\)là:

A. \(\dfrac{{ - 4x}}{{1 + x}}\)                      B. \(\dfrac{{ - 4x}}{{x - 1}}\)

C. \(\dfrac{{4x}}{{x - 1}}\)                          D. \(\dfrac{{4x}}{{x + 1}}\)

2. Thực hiện phép chia \({x^3} + 27\) cho \(3x - {x^2} - 9\) ta được thương là:

A. \(x + 3\)                              B. \( - x - 3\)

C. \(x - 3\)                               D. \( - x + 3\)

Câu 2 : (1,0 điểm) Trong các câu sau, câu nào đúng, câu nào sai:

a) Tứ giác có hai đường chéo vuông góc với nhau tại trung điểm mỗi đường là hình thoi.

b)Tứ giác có một cặp cạnh đối song song và cặp cạnh đối còn lại bằng nhau là hình thang cân.

c) Hai tam giác có diện tích bằng nhau thì hai tam giác đó bằng nhau.

d) Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

B. TỰ LUẬN (8,0 điểm)

Câu 1 (1,5 điểm):Phân tích các đa thức sau thành nhân tử:

a) \({x^2} - 9x - 9y - {y^2}\)

b) \(2xy - {x^2} - {y^2} + 16\)

c) \({x^3} - {x^2} - 6x\)

Câu 2 (2,5điểm):Cho biểu thức:\(A = \left( {\dfrac{{3{x^2}}}{{{x^2} - 4}} - \dfrac{3}{{x + 2}} + \dfrac{3}{{2 - x}}} \right):\dfrac{{x + 3}}{{x + 2}}\)

a) Rút gọn biểu thức A.

b) Tính giá trị biểu thức A khi \(\left| {x - 2} \right| = 4\).

c) Tìm giá trị nguyên của x để biểu thức A có giá trị là một số nguyên.

Câu 3 (3,5điểm):Cho hình chữ nhật ABCD. Kẻ AN và CM cùng vuông góc với BD (\(M,\,\,N \in BD\))

a) Chứng minh tứ giác ANCM là hình bình hành.

b)Gọi K là điểm đối xứng với điểm A qua N. Chứng minh MNKC là hình chữ nhật.

c) Tứ giác DKCB là hình gì? Tại sao?

d) Tia AM cắt tia KC tại P. Chứng minh các đường thẳng PN, AC, KM đồng quy.

Câu 4 (0,5 điểm):Cho x, y là hai số thực khác 0 thỏa mãn: \(2{x^2} + \dfrac{{{y^2}}}{4} + \dfrac{1}{{{x^2}}} = 4\).

Tìm giá trị lớn nhất và giá trị nhỏ nhất của \(A = 2016 + xy\)

Câu 1 (2,5 điểm):

Cho biểu thức \(P = \left( {\dfrac{1}{{x - 2}} - \dfrac{{{x^2}}}{{8 - {x^3}}}.\dfrac{{{x^2} + 2x + 4}}{{x + 2}}} \right):\dfrac{1}{{{x^2} - 4}}\)

a) Tìm điều kiện của x để P có nghĩa và rút gọn P.

b) Tìm giá trị nhỏ nhất của biểu thức P.

c) Tìm các số nguyên x để \(P \vdots \left( {{x^2} + 1} \right)\).

Câu 2 (2điểm):

Phân tích các đa thức sau thành nhân tử:

\(A\left( x \right) = 2{x^2} + x - 3\)

\(B\left( {a;b;c} \right) = \left( {a + b} \right)\left( {b + c} \right)\left( {c + a} \right) + abc\)

Câu 3 (1điểm):

Cho hai đa thức \(P\left( x \right) = {x^3} + ax + b\)và \(Q\left( x \right) = {x^2} - 3x + 2\). Xác định các hệ số a, b sao cho với mọi giá trị của x thì \(P\left( x \right) \vdots Q\left( x \right)\).

Câu 4 (3,5 điểm):

Cho hình thoi ABCD có góc D bằng \({60^o}\). Gọi E, H, G, Flần lượt là trung điểm của AB, BC, CD và DA.

a) Chứng minh tứ giác EFGH là hình chữ nhật.

b) Cho AG cắt HF tại J. Chứng minh rằng \(HF = 4FJ\).

c) Gọi I là trung điểm của FJ và P là giao điểm của EH và DB. Chứng minh IG vuông góc với IP.

d) Cho \(AB = 2cm\). Tính độ dài IP.

Câu 5 (1 điểm):

a) Cho ba số a, b, c thỏa mãn \(\left( {a + b + c} \right)\left( {ab + bc + ca} \right) = 2017\) và \(abc = 2017\).

Tính giá trị của biểu thức \(P = \left( {{b^2}c + 2017} \right)\left( {{c^2}a + 2017} \right)\left( {{a^2}b + 2017} \right)\).

b) (Dành riêng cho lớp 8A) Tìm các số tự nhiên x, n sao cho số \(p = {x^4} + {2^{4n + 2}}\) là một số nguyên tố.

Bài 1 (2 điểm)Thực hiện các phép tính:

Bài 2 (2 điểm)Phân tích đa thức thành nhân tử:

Bài 3 (2,5 điểm)Cho biểu thức: \(P = \dfrac{{2{x^2} - 1}}{{{x^2} + x}} - \dfrac{{x - 1}}{x} + \dfrac{3}{{x + 1}}\)

Bài 4 (3,5 điểm) Cho \(\Delta ABC\) vuông tại \(A,\,AB = 6\,cm,\,AC = 8\,cm\). Gọi \(M\) là trung điểm của đoạn \(BC\). Điểm \(D\) đối xứng với \(A\)  qua \(M\).

Bài 1.Phân tích đa thức \({x^2} + 4{y^2} + 4xy - 16\) thành nhân tử.

Bài 2.Thực hiện phép tính: \({{2x + 6} \over {3{x^2} - x}}:{{{x^2} + 3x} \over {1 - 3x}}.\)

Bài 3.Cho biểu thức \(P = {{8{x^3} - 12{x^2} + 6x - 1} \over {4{x^2} - 4x + 1}}.\)

a)Tìm điều kiện xác định của biểu thức P.

b)Chứng minh rằng mọi giá trị của x nguyên thì P nguyên.

Bài 4.Chứng minh rằng \(\left( {{x \over {{x^2} - 36}} - {{x - 6} \over {{x^2} + 6x}}} \right):{{2x - 6} \over {{x^2} + 6x}} + {x \over {6 - x}} =  - 1.\)

Bài 5.Tìm chiều cao AH của hình thang ABCD \(\left( {AB\parallel CD} \right)\) biết AB = 7cm, đường trung bình MN = 9cm và diện tích hình thang bằng \(45c{m^2}\).

Bài 6.Cho tam giác ABC vuông tại A \(\left( {AB < AC} \right).\) Gọi I là trung điểm của cạnh BC. Qua I vẽ IM vuông góc với AB tại M và IN vuông góc với AC tại N.

a)Chứng minh tư giác AMIN là hình chữ nhật.

b)Gọi D là điểm đối xứng của I qua N. Chứng minh tứ giác ADCI là hình thoi.

c)Cho AC = 20cm, BC = 25cm. Tính diện tích \(\Delta ABC.\)

d)Đường thẳng BN cắt cạnh DC tại K. Chứng minh: \({{DK} \over {DC}} = {1 \over 3}.\) 

Bài 1. Phân tích đa thức \({x^6} - {x^4} + 2{x^3} + 2{x^2}\) thành nhân tử.

Bài 2. Rút gọn : \(A = {{ab - 4b - 2a + 8} \over {2a + 8 - ab - 4b}}:{{2a - 8 - ab + 4b} \over {ab + 4b - 2a - 8}}.\)

Bài 3. Cho biểu thức : \(P = \left( {{{{x^2} - 2x} \over {2{x^2} + 8}} - {{2{x^2}} \over {8 - 4x + 2{x^2} - {x^3}}}} \right).\left( {1 - {1 \over x} - {2 \over {{x^2}}}} \right)\)        \(\left( {x \ne 0;x \ne 2} \right)\)

a) Rút gọn biểu thức P.

b) Tính giá trị của P với \(x \ne {1 \over 2}.\)

Bài 4. Tìm giá trị nguyên của x để giá trị của phân thức

\(Q = {{2{x^3} + {x^2} + 2x + 4} \over {2x + 1}}\) là số nguyên.

Bài 5. Cho tam giác ABC vuông tại A. Từ trung điểm I của cạnh BC, kẻ các đường thẳng song song với AB cắt AC tại N và song song với AC cắt AB tại M.

a) Chứng minh tứ giác AMIN là hình chữ nhật.

b) Dựng E là điểm đối xứng của I qua M, chứng minh NE đi qua trung điểm O của AM.

Bài 6. Cho hình vuông ABCD, trên cạnh DC lấy điểm E, từ A dựng đường thẳng vuông góc với AE tại A, đường này cắt đường thẳng BC tại F.

a) Chứng tỏ AF = AE.

b)Từ E dựng đường thẳng song song với đường thẳng AF và từ F dựng đường thẳng song song với đường thẳng AE, hai đường thẳng này cắt nhau tại G. Chứng tỏ AEGF là hình vuông.

c)Chứng tỏ ba đường thẳng BD, AG, EF đồng quy.

Bài 1. Phân tích đa thức \({a^3} + 3{a^2} + 3a + 1\) thành nhân tử.

Bài 2. Rút gọn và tính giá trị của biểu thức \(A = {{2x} \over {1 - {x^3}}} + {1 \over {{x^2} - x}} - {1 \over {{x^2} + x + 1}}\)   khi x = 10.

Bài 3. Cho biểu thức \(P = {2 \over {{x^4} - 1}} + {1 \over {1 - {x^2}}}.\)

a) Tìm điều kiện xác định của biểu thức P.

b) Chứng minh giá trị của P luôn âm với \(x \ne  \pm 1.\)

Bài 4. Chứng minh rằng biểu thức \(Q = \left( {{x^2} - 1} \right)\left( {{1 \over {x - 1}} - {1 \over {x + 1}} + 1} \right)\) luôn dương với \(x \ne  \pm 1.\)

Bài 5. Cho tứ giác ABCD. Hai đường chéo AC và BD vuông góc với nhau . Gọi M, N, P và Q lần lượt là trung điểm của các cạnh AB, BC, CD và DA.

a) Tứ giác MNPQ là hình gì? Vì sao ?

b) Để MNPQ là hình vuông thì tứ giác ABCD cần có điều kiện gì ?

Bài 6. Cho hình bình hành ABCD có AB = 2AD. Gọi E, F theo thứ tự là trung điểm của cạnh AB và CD.

a) Chứng tỏ tứ giác AECF là hình bình hành.

b) Chứng tỏ AF vuông góc với DE.

c) Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE, chứng tỏ EF = MN.

d) Tính tỉ số diện tích của \(\Delta BEF\) và diện tích hình bình hành ABCD.

Bài 1. Thực hiện phép tính:

a) \({{{x^2} - x + 1} \over {{x^2} - 1}}:{{{x^3} + 1} \over {3x - 3}}\)

b) \({1 \over {x + 1}} + {1 \over {x - 1}} + {2 \over {1 - {x^2}}}.\)

Bài 2. Phân tích đa thức \(3a - 3b - {a^2} + 2ab - {b^2}\) thành nhân tử.

Bài 3. Cho biểu thức \(A = {{{x^4} - 4{x^3} + 4{x^2}} \over {{x^3} - 4x}}.\)

a) Rút gọn biểu thức A.

b) Tìm giá trị x để giá trị của biểu thức A bằng 0.

Bài 4. Tìm m để \(P = {x^4} - {x^3} + 6{x^2} - x + m\) chia hết cho \(Q = 2{x^2} - x + 5.\)

Bài 5. Cho tam giác ABC, M là trung điểm của AC. Trên tia đối của tia MB lấy điểm F sao cho \(MF = MB.\) Gọi E là điểm đối xứng của F qua A và N là trung điểm của AB.

a) Chứng minh rằng E, N, C thẳng hàng.

b)\(\Delta ABC\) cân có điều kiện gì để EBCF là hình thang cân.

Bài 6. Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.

a) Gọi D là điểm đối xứng của A qua N. Chứng minh tứ giác ABDC là hình chữ nhật.

b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I. Chứng minh tứ giác ANCE là hình thoi.

c) Đường thẳng BC cắt DM và DI lần lượt tại G và \({G'}\). Chứng minh \(BG = C{G'}.\)

d) Cho AB = 6cm, AC = 8cm. Tính diện tích \(\Delta DG{G'}\).

Bài 1. Phân tích thành nhân tử:

a) \(9 - {x^2} + 6xy - 9{y^2}\)

b) \({x^4} - 2{x^2}.\)

Bài 2. Tìm m để \(P = {x^3} + 3{x^2} + mx + 8\) chia hết cho \(Q = x + 4.\)

Bài 3. Cho \({x \over y} = 10.\) Tính giá trị của biểu thức \(M = {{16{x^2} - 40xy} \over {8{x^2} - 24xy}}.\)

Bài 4. Cho biểu thức: \(A = {{5x - 6} \over {4 - {x^2}}} + {4 \over {x + 2}} + {2 \over {x - 2}}.\)

a) Tìm điều kiện xác định của biểu thức A.

b) Rút gọn biểu thức A.

Bài 5. Cho tam giác ABC cân tại A. Trên đường thẳng đi qua đỉnh A và song song với BC lấy hai điểm M và N sao cho A là trung điểm của MN (M, B cùng thuộc một nửa mặt phẳng bờ AC). Gọi H, I, K lần lượt là trung điểm của cạnh MB, BC và CN.

Chứng minh rằng tứ giác AHIK là hình thoi.

Bài 6. Cho tam giác ABC cân tại A, trung tuyến AM. Gọi D là điểm đối xứng với A qua M và K là trung điểm của MC, E là điểm đối xứng của D qua K.

a) Chứng minh tứ giác ABDC là hình thoi.

b) Chứng minh tứ giác AMCE là hình chữ nhật.

c) AM và BE cắt nhau tại I. Chứng minh rằng I là trung điểm của BE.

d) Chứng minh rằng AK, CI, EM đồng quy.

Bài 1. Phân tích đa thức thành nhân tử :

 a)\({x^2} + xy - x - y\)

b)\({a^2} - {b^2} + 8a + 16.\)

Bài 2.Tìm x, biết : a) \(4x\left( {x + 1} \right) + \left( {3 - 2x} \right)\left( {3 + 2x} \right) = 15\)

                       b)\(3x\left( {x - 20012} \right) - x + 20012 = 0.\)

Bài 3. Thực hiện phép tính :

a) \({1 \over {x\left( {x - y} \right)}} + {1 \over {y\left( {y - x} \right)}}\)

b) \({{x - 3} \over {x + 1}} - {{x + 2} \over {x - 1}} - {{8x} \over {1 - {x^2}}}.\)

Bài 4. Tính tổng \({x^4} + {y^4}\) biết \({x^2} + {y^2} = 18\) và \(xy = 5.\)

Bài 5. Cho tam giác ABC vuông tại A (AB < AC). M là trung điểm cạnh BC. Vẽ MD vuông góc với AB tại D và ME vuông góc với AC tại E.

a) Chứng minh tứ giác MDME là hình chữ nhật.

b) Chứng minh E là trung điểm của đoạn thẳng AC và tứ giác CMDE là hình bình hành.

c) Vẽ đường cao AH của tam giác ABC. Chứng minh tứ giác MHDE là hình thang cân.

d) Qua A vẽ đường thẳng song song với DH cắt DE tại K. Chứng minh HK vuông góc với AC.