Đọc hiểu - Đề số 30 - THPT
Lời giải
Bài Tập và lời giải
Thực hiện các phép đo cần thiết (chính xác đến từng mm) để tính diện tích hình \(ABCDE\) (h.\(152\)).

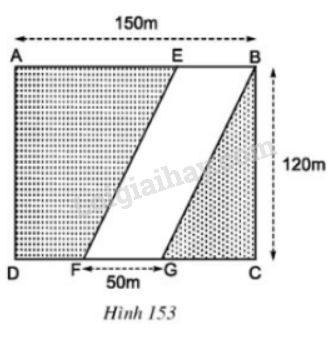
Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình \(153.\) Hãy tính diện tích phần con đường \(EBGF \;(EF // BG)\) và diện tích phần còn lại của đám đất .
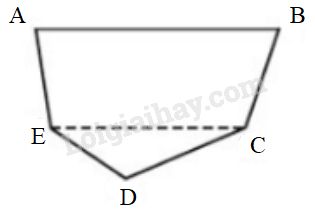
Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình \(154\), trong đó \(AB // CE\) và được vẽ tỉ lệ \(\dfrac{1}{5000}\)
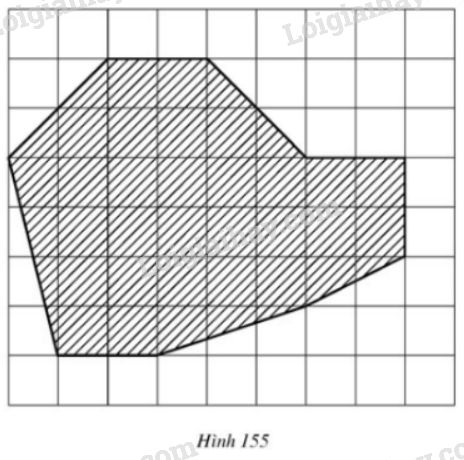
Tính diện tích thực của hồ nước có sơ đồ là phần gạch sọc trên hình \(155\) (cạnh của mỗi hình vuông là \(1\,cm\), tỉ lệ \(\dfrac{1}{10000}\) ).
Cho tứ giác ABCD. Gọi M là trung điểm của AB, N là trung điểm của CD. Chứng minh \({S_{BNDM}} = \dfrac{1}{2}{S_{ABCD}}.\)
Cho tam giác ABC, lấy P, Q lần lượt là trung điểm cạnh AB và AC. Kẻ BE, CF cùng vuông góc với PQ.
a)Chứng minh tứ giác BCFE là hình chữ nhật.
b)Chứng minh \({S_{BCFE}} = {S_{ABC}}.\)
Cho hình chữ nhật ABCD, từ M bất kì trên AB, kẻ đường thẳng song song với BC cắt CD tại N và đường chéo BD tại I. Qua I kẻ đường thẳng song song với AB cắt hai cạnh BC và AD lần lượt tại P và Q. Chứng minh rằng hai hình chữ nhật MIQA và NIPC có cùng diện tích
Cho hình chữ nhật ABCD có AB = 6cm, AC = 10 cm. Gọi O là giao điểm hai đường chéo AC và BD và M, N, P, Q lần lượt là trung điểm của OA, OB, OC, OD.
a) Tính \({S_{MNPQ}}.\)
b) Chứng minh rằng: \({S_{AMNB}} = {S_{CPQD}}.\)
Bài 1. Cho hình vuông ABCD, M là trung điểm của CD, N là trung điểm của AD. Gọi I là giao điểm của AM và BN.
Chứng minh rằng: \({S_{DMIN}} = {S_{AIB}}.\)
Bài 2. Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB.
Chứng minh rằng: \({S_{ABCD}} = 2{S_{EDC}}.\)
Cho hình thang ABCD \(\left( {AB//CD} \right)\). Gọi O là giao điểm của hai đường chéo AC và BD.
a) Chứng minh rằng: \({S_{AOD}} = {S_{BOC}}.\)
b) Gọi M là trung điểm của BC. Từ M kẻ đường thẳng song song với AD cắt AB tại E và DC tại F.
Chứng minh rằng: \({S_{ABCD}} = {S_{AEFD}}.\)
Cho hình thang ABCD \(\left( {AB// CD} \right).\) Gọi M, N lần lượt là trung điểm của các cạnh bên AD và BC, kẻ \(MH \bot CD\) (H thuộc CD) và MH cắt đường thẳng ABV tại I, kẻ \(NK \bot CD\) (K thuộc CD) và NK cắt AB tại I
Chứng minh: \({S_{ABCD}} = {S_{HKLI}}.\)
Gọi M, N theo thứ tự là các trung điểm của hai đáy AD và BC của hình thang ABCD. Từ điểm O tùy ý thuộc đoạn MN, kẻ đường thẳng song song với đáy hình thang, đường thảng này cắt các cạnh bên của hình thang tại E và F. Chứng minh rằng O là trung điểm của EF.
Cho hình bình hành ABCD, từ A và C kẻ AH, CK cùng vuông góc với đường chéo BD. Chứng minh rằng hai đa giác ABCH và ADCK có cùng diện tích.
Cho hình bình hành ABCD. Phân giác của \(\widehat A\) và \(\widehat C\) cắt đường chéo BD tại E và F. Chứng minh rằng hai đa giác ABCFE và ADCFE có diện tích bằng nhau
Cho hình vuông ABCD có cạnh a, giao điểm hai đường chéo là O. Một góc vuông \(\widehat {xOy}\) sao cho Ox cắt cạnh AB tại E, tia Oy cắt cạnh BC tại F.
Tính \({S_{OEBF}}\) theo a.
Cho hình chữ nhật ABCD. Lấy E, F, G, H lần lượt trên các cạnh AB, BC, CD sao cho tứ giác EFGH có hai đường chéo EG và FH vuông góc với nhau. Chứng minh: \({S_{EFGH}} \ge {1 \over 2}{S_{ABCD}}.\)
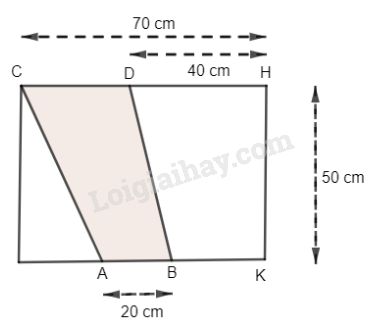
Tính diện tích phần tô màu trên hình vẽ.
Cho đa giác n – cạnh có diện tích S, các đường thẳng a, b, c cắt nhau tại A, B, C nằm trong tam giác sao cho mỗi đường thẳng chia đa giác thành hai phần có diện tích bằng nhau.
Chứng minh rằng \({S_{ABC}} \le \dfrac{1}{4}S.\)
Ngũ giác ABCDE có các đỉnh lần lượt theo thứ tự đó. Có các điều kiện sau: \(BD// AE;CH \bot AE\left( {H \in AE} \right).\) Gọi I là giao điểm của BD và CH.
Chứng minh rằng: \({S_{ABCDE}} = \dfrac{1}{ 2}\left( {BD.CH + AE.IH} \right).\)
