Đề số 48 - Đề thi thử THPT Quốc gia môn Toán

Câu 1: Trong không gian cho đường thẳng \(\Delta \) và điểm O. Qua O có mấy đường thẳng vuông góc với \(\Delta \) ?

A. \(1\)

B. \(3\)

C. Vô số

D. \(2\)

Câu 2: Tính đạo hàm của hàm số \(y =  - {x^7} + 2{x^5} + 3{x^3}.\)

A. \(y =  - {x^6} + 2{x^4} + 3{x^2}\)

B. \(y =  - 7{x^6} - 10{x^4} - 6{x^2}\)

C. \(y = 7{x^6} - 10{x^4} - 6{x^2}.\)

D. \(y =  - 7{x^6} + 10{x^4} + 9{x^2}.\)

Câu 3: Tìm \(I = \lim \dfrac{{8{n^5} - 2{n^3} + 1}}{{4{n^5} + 2{n^2} + 1}}.\)

A. \(I = 2\)

B. \(I = 8\)

C. \(I = 1\)

D. \(I = 4\)

Câu 4: Trong mặt phẳng tọa độ \(Oxy\), cho véctơ \(\overrightarrow v  = \left( { - 3;5} \right).\) Tìm ảnh của điểm \(A\left( {1;2} \right)\) qua phép tịnh tiến theo vectơ \(\overrightarrow v .\)

A. \(A'\left( {4; - 3} \right)\)

B. \(A'\left( { - 2;3} \right)\)

C. \(A'\left( { - 4;3} \right)\)

D. \(A'\left( { - 2;7} \right)\)

Câu 5: Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường \(y = f\left( x \right),\)trục Ox và hai đường thẳng \(x = a,x = b\) xung quanh trục Ox.

A. \(\pi \int\limits_a^b {{f^2}\left( x \right)dx} \)

B. \(\int\limits_a^b {{f^2}\left( x \right)dx} \)

C. \(\pi \int\limits_a^b {f\left( x \right)dx} \)

D. \(2\pi \int\limits_a^b {{f^2}\left( x \right)dx} \)

Câu 6: Nguyên hàm của hàm số \(f\left( x \right) = cos3x\)là:

A. \( - 3\sin 3x + C\)

B. \( - \dfrac{1}{3}\sin 3x + C\)

C. \( - \sin 3x + C\)

D. \(\dfrac{1}{3}\sin 3x + C\)

Câu 7: Hàm số \(y = {x^4} - 2{x^2} + 1\) có bao nhiêu điểm cực trị?

A. \(1\)

B. \(0\)

C. \(3\)

D. \(2\)

Câu 8: Số nào trong các số sau lớn hơn 1?

A. \({\log _{0,5}}\dfrac{1}{8}\)

B. \({\log _{0,2}}125\)

C. \({\log _{\dfrac{1}{6}}}36\)

D. \({\log _{0,5}}\dfrac{1}{2}\)

Câu 9: Tổng số đỉnh, số cạnh và số mặt của hình lập phương là:

A. \(16\)

B. \(26\)

C. \(8\)

D. \(24\)

Câu 10: Từ các chữ số 1; 2; 3 có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau đôi một?

A. \(8\)

B. \(6\)

C. \(9\)

D. \(3\)

Câu 11: Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?

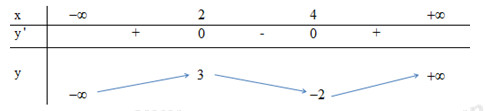
A. Hàm số đạt cực tiểu tại \(x =  - 2\)

B. Hàm số đạt cực tiểu tại \(x = 4\)

C. Hàm số đạt cực tiểu tại \(x = 2\)

D. Hàm số đạt cực đại tại \(x = 3\)

Câu 12: Cho hình chóp tam giác S.ABC với SA, SB, SC đôi một vuông góc và \(SA = SB = SC = a.\) Tính thể tích của khối chóp S. ABC.

A. \(\dfrac{1}{3}{a^3}\)

B. \(\dfrac{1}{2}{a^3}\)

C. \(\dfrac{1}{6}{a^3}\)

D. \(\dfrac{2}{3}{a^3}\)

Câu 13: Cho lăng trụ tam giác đều \(ABC.A'B'C'\)có tất cả các cạnh bằng 2a. Tính thể tích khối lăng trụ \(ABC.A'B'C'.\)

A. \({a^3}\sqrt 3 \)

B. \(\dfrac{{{a^3}\sqrt 3 }}{4}\)

C. \(\dfrac{{{a^3}\sqrt 3 }}{2}\)

D. \(2{a^3}\sqrt 3 \)

Câu 14: Phương trình \(\cos x =  - \dfrac{{\sqrt 3 }}{2}\) có tập nghiệm là

A. \(\left\{ { \pm \dfrac{\pi }{6} + k\pi ,k \in \mathbb{Z}} \right\}\)

B. \(\left\{ { \pm \dfrac{{5\pi }}{6} + k2\pi ,k \in \mathbb{Z}} \right\}\)

C. \(\left\{ { \pm \dfrac{\pi }{3} + k\pi ,k \in \mathbb{Z}} \right\}\)

D. \(\left\{ { \pm \dfrac{\pi }{3} + k2\pi ,k \in \mathbb{Z}} \right\}\)

Câu 15: Tập xác định của hàm số \(y = \dfrac{1}{{\sqrt {{x^2} - 4x + 5} }} + {\log _3}\left( {x - 4} \right)\) là

A. \(D = \left( { - 4; + \infty } \right)\)

B. \(D = \left[ { - 4; + \infty } \right)\)

C. \(D = \left( {4;5} \right) \cup \left( {5; + \infty } \right)\)

D. \(D = \left( {4; + \infty } \right)\)

Câu 16: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}}\) trên đoạn \(\left[ { - \dfrac{\pi }{2}; - \dfrac{\pi }{3}} \right]\)lần lượt là

A. \( - \dfrac{1}{2}; - \dfrac{{\sqrt 3 }}{2}\)

B. \( - \dfrac{{\sqrt 3 }}{2}; - 1\)

C. \( - \dfrac{{\sqrt 3 }}{2}; - 2\)

D. \( - \dfrac{{\sqrt 2 }}{2}; - \dfrac{{\sqrt 3 }}{2}\)

Câu 17: Tính đạo hàm của hàm số \(y = \left( {{x^2} - 2x + 2} \right){e^x}.\)

A. \(y' = \left( {{x^2} + 2} \right){e^x}\)

B. \(y' = {x^2}{e^x}\)

C. \(y' = \left( {2x - 2} \right){e^x}\)

D. \(y' =  - 2x{e^x}\)

Câu 18: Trong không gian với hệ trục tọa độ Oxyz, cho véctơ \(\overrightarrow a  = \left( {1; - 2;3} \right).\) Tìm tọa độ của véctơ \(\overrightarrow b \) biết rằng véctơ \(\overrightarrow b \) ngược hướng với véctơ \(\overrightarrow a \) và \(\left| {\overrightarrow b } \right| = 2\left| {\overrightarrow a } \right|\)

A. \(\overrightarrow b  = \left( {2; - 2;3} \right)\)

B. \(\overrightarrow b  = \left( {2; - 4;6} \right)\)

C. \(\overrightarrow b  = \left( { - 2;4; - 6} \right)\)

D. \(\overrightarrow b  = \left( { - 2; - 2;3} \right)\)

Câu 19: Hàm số \(y = \dfrac{{{x^4}}}{2} - \dfrac{{10{x^3}}}{3} + 2{x^2} + 16x - 15\) đồng biến trên khoảng nào sau đây?

A. \(\left( {2;4} \right)\)

B. \(\left( {2; + \infty } \right)\)

C. \(\left( {4; + \infty } \right)\)

D. \(\left( { - \infty ; - 1} \right)\)

Câu 20: Tính tích phân \(I = \int\limits_0^{\dfrac{\pi }{4}} {{{\tan }^2}x\,dx} \).

A. \(I = 1 - \dfrac{\pi }{4}\)

B. \(I = 2\)

C. \(I = \ln 2\)

D. \(I = \dfrac{\pi }{{12}}\)

Câu 21: Cho hàm số \(y = \,a{x^3} + b{x^2} + cx + d.\) Hàm số luôn đồng biến trên \(\mathbb{R}\) khi và chỉ khi

A. \(\left[ \begin{array}{l}a = b = 0,c > 0\\a > 0,{b^2} - 3ac \ge 0\end{array} \right.\)

B. \(a > 0,{b^2} - 3ac \le 0\)

C. \(\left[ \begin{array}{l}a = b = 0,c > 0\\a > 0,{b^2} - 3ac \le 0\end{array} \right.\)

D. \(\left[ \begin{array}{l}a = b = 0,c > 0\\a > 0,{b^2} - 4ac \le 0\end{array} \right.\)

Câu 22: Hình lập phương \(ABCD.A'B'C'D'\) cạnh a. Tính thể tích khối tứ diện ACB'D'.

A. \(\dfrac{{{a^3}}}{3}\)

B. \(\dfrac{{{a^3}}}{2}\)

C. \(\dfrac{{{a^3}}}{6}\)

D. \(\dfrac{{{a^3}}}{4}\)

Câu 23: Số \(6303268125\) có bao nhiêu ước số nguyên?

A. \(420\)

B. \(630\)

C. \(240\)

D. \(720\)

Câu 24: Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} =  - 1\), công bội \(q =  - \dfrac{1}{{10}}.\) Hỏi \(\dfrac{1}{{{{10}^{2017}}}}\) là số hạng thứ mấy của \(\left( {{u_n}} \right)?\)

A. Số hạng thứ \(2018\)

B. Số hạng thứ \(2017\)

C. Số hạng thứ \(2019\)

D. Số hạng thứ \(2016\)

Câu 25: Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{7x - 2}}{{{x^2} - 4}}\) là

A. \(2\)

B. \(4\)

C. \(1\)

D. \(3\)

Câu 26: Cho cấp số cộng \(\left( {{u_n}} \right)\) có\({u_4} =  - 12,{u_{14}} = 18\). Tính tổng 16 số hạng đầu tiên của cấp số cộng này.

A. \({S_{16}} =  - 24\)

B. \({S_{16}} = 26\)

C. \({S_{16}} =  - 25\)

D. \({S_{16}} = 24\)

Câu 27: Cho hình chóp \(S.ABCD\)có đáy là hình vuông cạnh a. Hình chiếu của S trên mặt phẳng (ABCD) trùng với trung điểm của cạnh AB. Cạnh bên \(SD = \dfrac{{3a}}{2}.\) Tính thể tích khối chóp \(S.ABCD\) theo a.

A. \(\dfrac{1}{3}{a^3}\)

B. \(\dfrac{{\sqrt 3 }}{3}{a^3}\)

C. \(\dfrac{{\sqrt 5 }}{3}{a^3}\)

D. \(\dfrac{{\sqrt 2 }}{3}{a^3}\)

Câu 28: Cho hàm số \(f\left( x \right) = \dfrac{{{x^2}}}{{ - x + 1}}.\) Tìm \({f^{\left( {30} \right)}}\left( x \right).\)

A. \({f^{\left( {30} \right)}}\left( x \right) =  - 30!{\left( {1 - x} \right)^{ - 30}}\)

B. \({f^{\left( {30} \right)}}\left( x \right) = 30!{\left( {1 - x} \right)^{ - 31}}\)

C. \({f^{\left( {30} \right)}}\left( x \right) = 30!{\left( {1 - x} \right)^{ - 30}}\)

D. \({f^{\left( {30} \right)}}\left( x \right) =  - 30!{\left( {1 - x} \right)^{ - 31}}\)

Câu 29: Cần phải thiết kế các thùng dạng hình trụ có nắp đựng nước sạch có dung tích \(V\left( {c{m^3}} \right).\) Hỏi bán kính \(R\left( {cm} \right)\)của đáy hình trụ nhận giá trị nào sau đây để tiết kiệm vật liệu nhất?

A. \(R = \sqrt[3]{{\dfrac{{3V}}{{2\pi }}}}\)

B. \(R = \sqrt[3]{{\dfrac{V}{\pi }}}\)

C. \(R = \sqrt[3]{{\dfrac{V}{{4\pi }}}}\)

D. \(R = \sqrt[3]{{\dfrac{V}{{2\pi }}}}\)

Câu 30: Tính diện tích xung quanh hình nón tròn xoay ngoại tiếp tứ diện đều cạnh bằng a.

A. \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 3 }}{3}\)

B. \({S_{xq}} = \dfrac{{\pi {a^2}}}{3}\)

C. \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 2 }}{3}\)

D. \({S_{xq}} = \dfrac{{\pi {a^2}\sqrt 3 }}{6}\)

Câu 31: Cho hình chóp tứ giác đều có tất cả các cạnh đều bằng a. Tính côsin của góc giữa mặt bên và mặt đáy.

A. \(\dfrac{1}{{\sqrt 3 }}\)

B. \(\dfrac{1}{2}\)

C. \(\dfrac{1}{{\sqrt 2 }}\)

D. \(\dfrac{1}{3}\)

Câu 32: Tìm một nguyên hàm \(F\left( x \right)\) của hàm số \(f\left( x \right) = a\,x + \dfrac{b}{{{x^2}}}\left( {x \ne 0} \right)\) biết rằng  

A. \(F\left( x \right) = \dfrac{{3{x^2}}}{4} + \dfrac{3}{{2x}} + \dfrac{7}{4}\)

B. \(F\left( x \right) = \dfrac{{3{x^2}}}{4} - \dfrac{3}{{2x}} - \dfrac{7}{4}\)   

C. \(F\left( x \right) = \dfrac{{3{x^2}}}{2} + \dfrac{3}{{4x}} - \dfrac{7}{4}\)

D. \(F\left( x \right) = \dfrac{{3{x^2}}}{2} - \dfrac{3}{{4x}} - \dfrac{1}{2}\)

Câu 33: Trong không gian với hệ trục tọa độ Oxyz cho hai điểm \(A\left( {l;0; - 3} \right),{\rm{ }}B\left( { - 3; - 2; - 5} \right).\) Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức \(A{M^2} + B{M^2} = 30\) là một mặt cầu\(\left( S \right)\). Tọa độ tâm I và bán kính R của mặt cầu \(\left( S \right)\)là:

A. \(I\left( { - 2; - 2; - 8} \right);R = 3\)

B. \(I\left( { - 1; - 1; - 4} \right);R = \sqrt 6 \)        

C. \(I\left( { - 1; - 1; - 4} \right);R = 3\)

D. \(I\left( { - 1; - 1; - 4} \right);R = \dfrac{{\sqrt {30} }}{2}\)

Câu 34: Cho hàm số \(y = f\left( x \right) = \dfrac{{2\sqrt {1 + x}  - \sqrt[3]{{8 - x}}}}{x}.\) Tính \(\mathop {\lim }\limits_{x \to 0} \,f\left( x \right).\)

A. \(\dfrac{1}{{12}}\)

B. \(\dfrac{{13}}{{12}}\)

C. \( + \infty \)

D. \(\dfrac{{10}}{{11}}\)

Câu 35: Số nghiệm của phương trình \(2{x^2} + 2x - 9 = \left( {{x^2} - x - 3} \right){.8^{{x^2} + 3x - 6}} \)\(\,+ \left( {{x^2} + 3x - 6} \right){.8^{{x^2} - x - 3}}\)là:

A. \(1\)

B. \(3\)

C. \(2\)

D. \(4\)

Câu 36: Cho hình chóp \(S.ABCD\)có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy

\(SA = a\sqrt 2 .\) Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp \(S.AB'C'D'\) là:

A. \(V = \dfrac{{2{a^3}\sqrt 3 }}{9}\)

B. \(V = \dfrac{{2{a^3}\sqrt 2 }}{3}\)

C. \(V = \dfrac{{{a^3}\sqrt 2 }}{9}\)

D. \(V = \dfrac{{2{a^3}\sqrt 3 }}{3}\)

Câu 37: Cho cấp số cộng \(\left( {{u_n}} \right)\) biết \({u_5} = 18\) và \(4{S_n} = {S_{2n}}.\)Tìm số hạng đầu tiên \({u_1}\) và công sai d của cấp số cộng.

A. \({u_1} = 2,d = 4\)

B. \({u_1} = 2,d = 3\)

C. \({u_1} = 2,d = 2\)

D. \({u_1} = 3,d = 2\)

Câu 38: Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và D; SD vuông góc với mặt đáy \(\left( {ABCD} \right);{\rm{ }}AD = 2a;{\rm{ }}SD = a\sqrt 2 .\) Tính khoảng cách giữa đường thẳng CD và mặt phẳng (SAB).

A. \(\dfrac{{2a}}{{\sqrt 3 }}\)

B. \(\dfrac{a}{{\sqrt 2 }}\)

C. \(a\sqrt 2 \)

D. \(\dfrac{{a\sqrt 3 }}{2}\)

Câu 39: Trong hình hộp \(ABCD.A'B'C'D'\)có tất cả các cạnh đều bằng nhau. Trong các mệnh đề sau, mệnh đề nào sai?

A. \(BB' \bot BD\)

B. \(A'C' \bot BD\)

C. \(A'B \bot DC'\)

D. \(BC' \bot A'D\)

Câu 40: Cho đồ thị hàm số \(\left( C \right):y = f\left( x \right) = 2{x^3} - 3{x^2} + 5.\) Từ điểm \(A\left( {\dfrac{{19}}{{12}};4} \right)\) kẻ được bao nhiêu tiếp tuyến tới \(\left( C \right)\).

A. \(1\)

B. \(2\)

C. \(3\)

D. \(4\)

Câu 41: Trong không gian với hệ tọ độ Oxyz, cho bốn điểm\(A\left( {1;0;0} \right),{\rm{ }}B\left( {0;1;0} \right),\) \(C\left( {0;0;1} \right),{\rm{ }}D\left( {0;0;0} \right).\) Hỏi có bao nhiêu điểm cách đều bốn mặt phẳng \(\left( {ABC} \right),\left( {BCD} \right),\)\(\left( {CDA} \right),\left( {DAB} \right)?\)

A. \(4\)

B. \(5\)

C. \(1\)

D. \(8\)

Câu 42: Với một đĩa phẳng hình tròn bằng thép bán kính R, phải làm một cái phễu bằng cách cắt đi một hình quạt của đĩa này và gấp phần còn lại thành một hình nón. Gọi độ dài cung tròn của hình quạt còn lại là x. Tìm x để thể tích khối nón tạo thành nhận giá trị lớn nhất.

A. \(x = \dfrac{{2\pi R\sqrt 6 }}{3}\)

B. \(x = \dfrac{{2\pi R\sqrt 2 }}{3}\)

C. \(x = \dfrac{{2\pi R\sqrt 3 }}{3}\)

D. \(x = \dfrac{{\pi R\sqrt 6 }}{3}\)

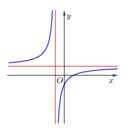
Câu 43: Hình vẽ bên dưới là đồ thị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}.\) Mệnh đề nào sau đây là đúng?

A. \(bd < 0,ab > 0\)

B. \(ad < 0,ab < 0\)

C. \(ad > 0,ab < 0\)

D. \(bd > 0,ad > 0\)

Câu 44: Tìm tất cả các giá trị thực của tham số m để hàm số \(y = \dfrac{{\cos x - 2}}{{\cos x - m}}\) nghịch biến trên

khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\).

A. \(m > 2\)

B. \(m \le 0\) hoặc \(1 \le m < 2\)

C. \(m \le 2\)

D. \(m \le 0\)

Câu 45: Một ô tô đang chạy với tốc độ 10(m/s) thì người lái đạp phanh, từ thời điểm đó ô tô chuyển động chậm dần đều với \(v\left( t \right) =  - 5t + 10\left( {m/s} \right),\)trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?

A. \(8m\)

B. \(10m\)

C. \(5m\)

D. \(20m\)

Câu 46: Gọi m là số thực dương sao cho đường thẳng \(y = m + 1\)cắt đồ thị hàm số \(y = {x^4} - 3{x^2} - 2\) tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng?

A. \(m \in \left( {\dfrac{7}{9};\dfrac{9}{4}} \right)\)

B. \(m \in \left( {\dfrac{1}{2};\dfrac{3}{4}} \right)\)

C. \(m \in \left( {\dfrac{3}{4};\dfrac{5}{4}} \right)\)

D. \(m \in \left( {\dfrac{5}{4};\dfrac{7}{4}} \right)\)

Câu 47: Từ các chữ số \(0,{\rm{ }}1,{\rm{ }}2,{\rm{ }}3,{\rm{ }}5,{\rm{ }}8\) có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số 3?

A. \(36\)số

B. \(108\)số

C. \(228\)số

D. \(144\)số

Câu 48: Trong không gian với hệ tọa độ Oxyz, cho hai điểm \(A\left( {0;2; - 4} \right),{\rm{ }}B\left( { - 3;5;2} \right).\) Tìm tọa độ điểm M sao cho biểu thức \(M{A^2} + 2M{B^2}\) đạt giá trị nhỏ nhất.

A. \(M\left( { - 1;3; - 2} \right)\)

B. \(M\left( { - 2;4;0} \right)\)

C. \(M\left( { - 3;7; - 2} \right)\)

D. \(M\left( { - \dfrac{3}{2};\dfrac{7}{2}; - 1} \right)\)

Câu 49: Tìm tập các giá trị thực của tham số m để phương trình \(4{\left( {\sqrt 2  + 1} \right)^x} + {\left( {\sqrt 2  - 1} \right)^x} - m = 0\) có đúng hai nghiệm âm phân biệt.

A. \(\left( {2;4} \right)\)

B. \(\left( {3;5} \right)\)

C. \(\left( {4;5} \right)\)

D. \(\left( {5;6} \right)\)

Câu 50 : Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại \(B,{\rm{ }}AB = BC = a\sqrt 3 \),

\(\widehat {SAB} = \widehat {SCB} = {90^ \circ }\) và khoảng cách từ điểm A đến mặt phẳng (SBC) bằng \(a\sqrt 2 .\) Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC theo a.

A. \(S = 4\pi {a^2}\)

B. \(S = 8\pi {a^2}\)

C. \(S = 12\pi {a^2}\)

D. \(S = 16\pi {a^2}\)