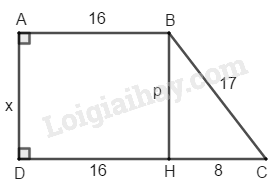
Kẻ \(BH ⊥ CD\)
\(\widehat A = {90^0},\widehat D = {90^0},\widehat {BHD} = {90^0}\)
Suy ra: Tứ giác \(ABHD\) là hình chữ nhật (vì có ba góc vuông)
\(⇒ AB = DH, BH = AD\)
\(HC = CD – DH\)
\(CD \,– AB = 24 – 16 = 8 \,(cm)\)
Trong tam giác vuông \(BHC,\) theo định lí Pi-ta-go ta có:
\(\eqalign{ & B{C^2} = B{H^2} + H{C^2} \cr & \Rightarrow B{H^2} = B{C^2} - H{C^2} \cr & B{H^2} = {17^2} - {8^2} = 289 - 64 = 225 \cr & BH = \sqrt {225} = 15(cm) \cr & x = AD = BH = 15(cm) \cr} \)