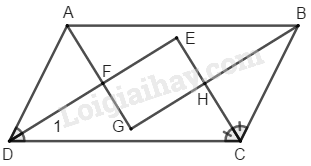
Gọi \(G,\, H,\, E, \,K\) lần lượt là giao điểm của các đường phân giác của \(\widehat A\) và\(\widehat B\); \(\widehat B\) và\(\widehat C\); \(\widehat C\) và\(\widehat D\); \(\widehat D\) và\(\widehat A\).
Ta có: \(\widehat {ADF} = \eqalign{1 \over 2}\widehat {ADC}\) (gt)
\(\widehat {DAF} =\eqalign {1 \over 2}\widehat {DAB}\) (gt)
\(\widehat {ADC} + \widehat {DAB} = {180^0}\) (hai góc trong cùng phía)
Suy ra: \(\widehat {ADF} + \widehat {DAF} = \eqalign{1 \over 2}\left( {\widehat {ADC} + \widehat {DAB}} \right)\) \(=\eqalign {1 \over 2}{.180^0} = {90^0}\)
Trong \(∆ AFD\) ta có:
\(\widehat {AFD} = {180^0} - \left( {\widehat {ADF} + \widehat {DAF}} \right) \) \(= {180^0} - {90^0} = {90^0}\)
\(\widehat {EFG} = \widehat {AFD}\) (đối đỉnh)
\(\eqalign{ & \Rightarrow \widehat {EFG} = {90^0} \cr & \widehat {GAB} = \eqalign{1 \over 2}\widehat {DAB}(gt) \cr & \widehat {GBA} = {1 \over 2}\widehat {CBA}(gt) \cr} \)
\(\widehat {DAB} + \widehat {CBA} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {GBA} + \widehat {GAB}\) \(= \eqalign{1 \over 2}\left( {\widehat {DAB} + \widehat {CBA}} \right)\) \(= \eqalign{1 \over 2}{.180^0} = {90^0}\)
Trong \(∆ AGB\) ta có: \(\widehat {AGB} = {180^0} - \left( {\widehat {GAB} + \widehat {GBA}} \right) \) \(= {180^0} - {90^0} = {90^0}\)
hay \(\widehat G = {90^0}\)
\(\eqalign{ & \widehat {EDC} = \eqalign{1 \over 2}\widehat {ADC}(gt) \cr & \widehat {ECD} =\eqalign {1 \over 2}\widehat {BCD}(gt) \cr} \)
\(\widehat {ADC} + \widehat {BCD} = {180^0}\) (hai góc trong cùng phía)
\( \Rightarrow \widehat {EDC} + \widehat {ECD} \) \(= \eqalign{1 \over 2}\left( {\widehat {ADC} + \widehat {BCD}} \right) \) \(= \eqalign{1 \over 2}{.180^0} = {90^0}\)
Trong \(∆ EDC\) ta có: \(\widehat {DEC} = {180^0} - \left( {\widehat {EDC} + \widehat {ECD}} \right)\) \(= {180^0} - {90^0} = {90^0}\) hay \(\widehat E = {90^0}\)