\(BH ⊥ DE\) (gt)
\(CK ⊥ DE\) (gt)
Suy ra \(BH // CK\) nên tứ giác \(BHKC\) là hình thang
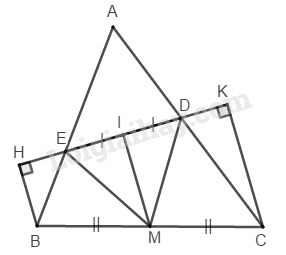
Ta có: Gọi \(M\) là trung điểm của \(BC,\) \(I\) là trung điểm của \(DE\)
Trong tam giác \(BDC\) vuông tại \(D\) có \(DM\) là trung tuyến thuộc cạnh huyền \(BC.\)
\(⇒ DM = \dfrac{1}{2} BC\) (tính chất tam giác vuông)
Trong tam giác \(BEC\) vuông tại \(E\) có \(EM\) là đường trung tuyến thuộc cạnh huyền \(BC.\)
\(⇒ DM = \dfrac{1}{2} BC\) (tính chất tam giác vuông)
Suy ra: \(DM = EM\) nên \(∆ MDE\) cân tại \(M\)
\(MI\) là đường trung tuyến nên \(MI\) là đường cao \(⇒ MI ⊥ DE\)
Suy ra: \(MI // BH // CK\)
\(BM = MC\)
Suy ra: \(HI = IK\) (tính chất đường trung bình hình thang)
\(⇒ HE + EI = ID + DK\)
mà \(EI = ID\) ( theo cách vẽ)
\(⇒ HE = DK\)