Bài 2. Các quy tắc tính đạo hàm

Tính đạo hàm của mỗi hàm số sau tại điểm x₀ được cho kèm theo

a. \(y = 7 + x - {x^2},{x_0} = 1\)

b. \(y = {x^3} - 2x + 1,{x_0} = 2\)

c. \(y = 2{x^5} - 2x + 3,{x_0} = 1\)

Tìm đạo hàm của mỗi hàm số sau (a và b là hằng số)

a. \(y = {x^5} - 4{x^3} + 2x - 3\sqrt x \)

b. \(y = {1 \over 4} - {1 \over 3}x + {x^2} - 0,5{x^4}\)

c. \(y = {{{x^4}} \over 4} - {{{x^3}} \over 3} + {{{x^2}} \over 2} - x + {a^3}\)

d. \(y = {{ax + b} \over {a + b}}\)

Tìm đạo hàm của mỗi hàm số sau :

a. \(y = \left( {{x^7} + {x}} \right)^2\)

b. \(y = \left( {{x^2} + 1} \right)\left( {5 - 3{x^2}} \right)\)

c. \(y = {{2x} \over {{x^2} - 1}}\)

d. \(y = {{5x - 3} \over {{x^2} + x + 1}}\)

e. \(y = {{{x^2} + 2x + 2} \over {x + 1}}\)

f. \(y = x\left( {2x - 1} \right)\left( {3x + 2} \right)\)

Tìm đạo hàm của mỗi hàm số sau

a. \(y = {\left( {x - {x^2}} \right)^{32}}\)

b. \(y = {1 \over {x\sqrt x }}\)

c. \(y = {{1 + x} \over {\sqrt {1 - x} }}\)

d. \(y = {x \over {\sqrt {{a^2} - {x^2}} }}\) (a là hằng số)

Cho hàm số \(f\left( x \right) = \sqrt {{x^2} - 2x} \) . Hãy giải bất phương trình \(f'\left( x \right) \le f\left( x \right)\)

Cho hàm số \(f\left( x \right) = {x^3} - 3{x^2} + 2.\) Hãy giải bất phương trình :

a. \(f'\left( x \right) > 0\)

b. \(f'\left( x \right) \le 3\)

Tìm các nghiệm của phương trình sau (làm tròn kết quả nghiệm gần đúng đến hàng phần nghìn)

a. \(f'\left( x \right) = 0\,\text{ với }\,f\left( x \right) = {{{x^3}} \over 3} - 2{x^2} - 6x - 1\)

b. \(f'\left( x \right) =  - 5\,\text{ với }\,f\left( x \right) = {{{x^4}} \over 4} - {x^3} - {{3{x^2}} \over 2} - 3.\)

Tính đạo hàm của mỗi hàm số sau

a. \(y = {{2x + 3} \over {{x^2} - 5x + 5}}\)

b. \(y = {1 \over {{{\left( {{x^2} - x + 1} \right)}^5}}}\)

c. \(y = {x^2} + x\sqrt x  + 1\)

d. \(y = \left( {x + 1} \right){\left( {x + 2} \right)^2}{\left( {x + 3} \right)^3}\)

e. \(y = \sqrt {{{{x^2} + 1} \over x}} \)

Viết phương trình tiếp tuyến của đồ thị hàm số

a. \(y = {{x - 1} \over {x + 1}}\), biết hoành độ tiếp điểm là x₀ = 0

b. \(y = \sqrt {x + 2} ,\) biết tung độ tiếp điểm là y₀ = 2.

Viết phương trình tiếp tuyến của parabol \(y = {x^2}\) , biết rằng tiếp tuyến đó đi qua điểm A(0 ; -1).

Hướng dẫn : Trước hết viết phương trình tiếp tuyến tại điểm có hoành độ x₀ thuộc parabol đã cho. Sau đó tìm x₀ để tiếp tuyến đi qua điểm A (chú ý rằng điểm A không thuộc parabol).

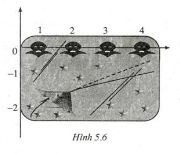
Hình 5.6 thể hiện màn hình của một trò chơi điện tử. Một máy bay xuất hiện ở bên trái màn hình rồi bay sang phải theo một quỹ đạo (C) là đồ thị của hàm số \(y = f\left( x \right)\) , trong đó \(f\left( x \right) =  - 1 - {1 \over x},\left( {x > 0} \right).\) Biết rằng tên lửa được bắn ra từ máy bay tại một điểm thuộc (C) sẽ bay theo phương tiếp tuyến của (C) tại điểm đó. Tìm hoành độ các điểm thuộc (C) sao cho tên lửa bắn ra từ đó có thể bắn trúng một trong bốn mục tiêu nằm ở trên màn hình có tọa độ (1 ; 0), (2 ; 0), (3 ; 0) và (4 ; 0) (làm tròn kết quả đến hàng phần vạn)

Một viên đạn được bắn lên từ mặt đất theo phương thẳng đứng với tốc độ ban đầu v₀ = 196 m/s (bỏ qua sức cản của không khí). Tìm thời điểm tại đó tốc độ của viên đạn bằng 0. Khi đó, viên đạn cách mặt đất bao nhiêu mét ?