Bài 3. Đạo hàm của các hàm số lượng giác

Tìm các giới hạn sau :

a. \(\mathop {\lim }\limits_{x \to 0} {{\tan 2x} \over {\sin 5x}}\)

b. \(\mathop {\lim }\limits_{x \to 0} {{1 - {{\cos }^2}x} \over {x\sin 2x}}\)

c. \(\mathop {\lim }\limits_{x \to 0} {{1 + \sin x - \cos x} \over {1 - \sin x - \cos x}}\)

Tìm đạo hàm của các hàm số sau :

a. \(y = 5\sin x - 3\cos x\)

b. \(y = \sin \left( {{x^2} - 3x + 2} \right)\)

c. \(y = \cos \sqrt {2x + 1} \)

d. \(y = 2\sin 3x\cos 5x\)

e. \(y = {{\sin x + \cos x} \over {\sin x - \cos x}}\)

f. \(y = \sqrt {\cos 2x} \)

Chứng minh rằng hàm số \(y = {\sin ^6}x + {\cos ^6}x + 3{\sin ^2}x{\cos ^2}x\) có đạo hàm bằng 0.

Đề bài

Tìm đạo hàm của các hàm số sau :

a. \(y = \tan {{x + 1} \over 2}\)

b. \(y = \cot \sqrt {{x^2} + 1} \)

c. \(y = {\tan ^3}x + \cot 2x\)

d. \(y = \tan 3x - \cot 3x\)

e. \(y = \sqrt {1 + 2\tan x} \)

f. \(y = x\cot x\)

Chứng minh rằng :

a. Hàm số y = tanx thỏa mãn hệ thức \(y' - {y^2} - 1 = 0\)

b. Hàm số y = cot2x thỏa mãn hệ thức \(y' + 2{y^2} + 2 = 0\)

Đề bài

Tìm đạo hàm của mỗi hàm số sau :

a. \(\displaystyle y = {{\sin x} \over x} + {x \over {{\mathop{\rm sinx}\nolimits} }}\)

b. \(\displaystyle y = {{{{\sin }^2}x} \over {1 + \tan 2x}}\)

c. \(y = \tan \left( {\sin x} \right)\)

d. \(y = x\cot \left( {{x^2} - 1} \right)\)

e. \(\displaystyle y = {\cos ^2}\sqrt {{\pi  \over 4} - 2x} \)

f. \(y = x\sqrt {\sin 3x} \)

Tính \(f'\left( \pi  \right)\) nếu \(f\left( x \right) = {{\sin x - x\cos x} \over {\cos x - x\sin x}}\)

Giải phương trình y’ = 0 trong mỗi trường hợp sau : 

a. y= sin2x - 2cosx

b. y = 3sin2x + 4cos2x + 10x

c. \(y = {\cos ^2}x + \sin x\)

d. \(y = \tan x + \cot x\)

Cho hàm số \(f\left( x \right) = 2{\cos ^2}\left( {4x - 1} \right)\). Chứng minh rằng với mọi x ta có \(\left| {f'\left( x \right)} \right| \le 8.\) Tìm các giá trị của x để đẳng thức xảy ra.

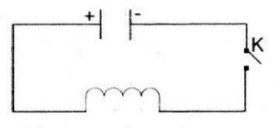
Cho mạch điện như hình 5.7. Lúc đầu tụ điện có điện tích Q₀. Khi đóng khóa K, tụ điện phóng điện qua cuộn dây ; điện tích q của tụ điện phụ thuộc vào thời gian t theo công thức \(q\left( t \right) = {Q_0}\sin \omega t.\) Trong đó, ω là tốc độ góc. Biết rằng cường độ I(t) của dòng điện tại thời điểm t được tính theo công thức \(I\left( t \right) = q'\left( t \right)\) Cho biết \({Q_0} = {10^{ - 8}}\,\text{ và }\,\omega  = {10^6}\pi \,rad/s.\) Hãy tính cường độ của dòng điện tại thời điểm t = 6s (tính chính xác đến 10^-5 mA)

Cho hàm số \(y = {\cos ^2}x + m\sin x\) (m là tham số) có đồ thị là (C). Tìm m trong mỗi trường hợp sau:

a. Tiếp tuyến của (C) tại điểm với hoành độ \(x = π\) có hệ số góc bằng 1

b. Hai tiếp tuyến của (C) tại các điểm có hoành độ \(x =  - {\pi  \over 4}\)  và \(x = {\pi  \over 3}\) song song hoặc trùng nhau.